
Introduction
Confounding and effect modification are among the most important concepts in epidemiology. These two central concepts, while closely related, are distinctly separate phenomena1. In view of the appropriate growing attention to sex-specific aspects in the prevention, treatment, and prognosis of cardiovascular disease, researchers are increasingly asked to take sex into consideration when reporting their findings. This article provides a simple introduction to the two concepts of confounding and effect modification, using sex as an example. There is, of course, much more to be said about these complex concepts than the simple approach taken in this article. The illustrative examples provided in this article are not necessarily specific to sex and could be applied to any other variable.
Confounding
Whilst it is desirable that the results in an epidemiological study reveal the true association between an exposure and an outcome, it should not be discarded that such an association might in fact be due to the presence of another factor. Alternatively, the apparent lack of an association between an exposure and an outcome could also result from failure to control for another factor. Such a third factor is referred to as a confounder. The confounding factor is a variable that: 1) is associated with the exposure of interest; 2) is a risk factor for the outcome under study, independently of the exposure of interest (in other words, it is associated with the outcome among unexposed); 3) is not caused by the exposure of interest, i.e., it is not an intermediate factor in the causal pathway between the exposure and the outcome (Figure 1). To assess whether a potential confounding variable is associated with the exposure of interest and with the outcome under study, some investigators perform formal statistical tests of hypothesis and conclude based on the statistical significance. Others, however, discard the statistical significance and regard a variable as a confounder if there is a clinically meaningful relationship between the potential confounder and the exposure of interest and between the potential confounder and the outcome under study.
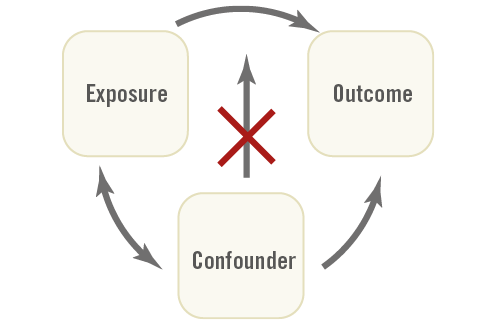
Figure 1. Schematic figure explaining confounding.
Confounding is referred to as a confusion or mixing of effects. The distortion of the estimated association between an exposure and an outcome depends on the direction of the association between the confounding factor and the exposure and outcome of interest. Consequently, a confounder can result in exaggeration (overestimation) of the true magnitude of the association between the exposure and the outcome (positive confounder). It can also lead to underestimation and obscuring part or all of the association between the exposure and the outcome (negative confounder). A confounder can even change the apparent direction of the association between the exposure and the outcome2.
Confounding arises from unequal distribution of a risk factor (i.e., the confounder) between the groups being compared on the exposure of interest (i.e., exposed and unexposed groups). To inform the study design and to allow proper data collection, investigators should think beforehand about the potential confounders3. To prevent confounding, several methods are suggested that may be applied to the study design: randomisation, restriction, and matching. Randomisation is the random assignment of subjects to experimental groups and can only be used in experiments2. Restriction implies selecting subjects for the study who have (nearly) the same value for the confounding factor2. The third method is matching the subjects in the exposed and unexposed groups in pairs for potential confounders. Matching is not a preferred method in addressing confounding and has even been suggested to introduce confounding in certain circumstances2.
Effect measure modification
Unlike confounding, effect modification (or interaction) is a biological phenomenon in which the exposure has a different impact in different circumstances. In this situation, the association between the exposure of interest and the outcome under study varies by the level (or across the strata) of another variable. This is called the heterogeneity of effect (vs. homogeneity). This other variable is an effect modifier. A distinction is sometimes made between this biological interaction and statistical interaction. If there is no bias, so that the observed associations validly estimate the causal effect of interest, the definition of effect-measure modification or heterogeneity of effect is equivalent to the definition of statistical interaction4. Statistical interaction is simply a departure from the underlying form of a statistical model and can be measured in two ways: as a relative risk (or rate ratio) or as a risk difference (or rate difference)2. To assess statistical interaction, a comparison is made between the observed and the expected joint effects of a risk factor and a third variable (the potential effect modifier). Statistical interaction is considered to be present when the observed joint effects of the risk factor and the third variable differ from the expected effect on the basis of their independent effects. Depending on the scale, statistical interaction is expressed as either the additive interaction or multiplicative interaction. Additive interaction is defined as deviation from an additive joint effect when risk difference is used as the measure of effect. Multiplicative interaction is defined as deviation from a multiplicative joint effect when risk ratio is used as the measure of effect. If there is no interaction, the observed joint effect of the risk factor and the third variable is almost equal to the sum of their independent effects based on an additive or a multiplicative scale. Positive interaction (synergism) or negative interaction (antagonism) occurs if the observed joint effect of the risk factor and the third factor is greater or smaller than the expected effect based on an additive or a multiplicative model.
Analytical approaches
A large portion of epidemiologic literature is concerned with methods regarding treating the confounders or effect modifiers. Two of the most common approaches to address confounding and effect modification are stratification and modelling (or multivariate analysis). In this article, we simply note that the most fundamental methods rely on stratification.
In stratified analysis, the observations are divided into groups based on each level (or combination of levels) of the factor we want to control for. Subsequently, the association between the exposure of interest and the outcome under study is examined separately within each group. In this manner, we may be able to observe the association between the exposure of interest and the outcome under study without interference from the stratification variable.
Suppose that we are interested in the risk of coronary heart disease (CHD) associated with smoking. For this purpose, we have data from a hypothetical nested case-control study. The crude odds ratio (OR) from this hypothetical study is 2.5. We now want to control the association between smoking and CHD for sex. Sex can potentially be a confounding factor or an effect modifier, as can any other variable. Table 1 shows the crude and stratum-specific ORs for men and women and illustrates four possible scenarios.
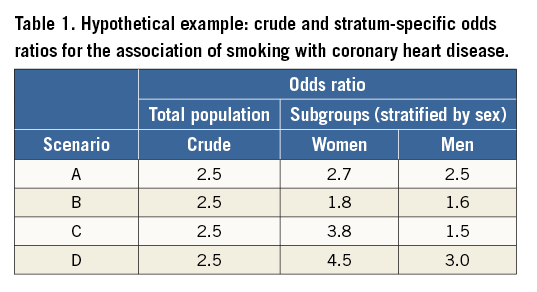
The crude OR for CHD is 2.5, meaning that smokers have a greater risk of CHD, compared to non-smokers. When we stratify by sex, this association is apparent in both sexes but more so among women. In scenario A, there is a slight difference between the two strata of men and women. Although the robust judgement should be based on proper statistical tests for comparison of the two ORs, the difference seems insufficient to warrant attention and might be attributable to random variation. While the stratum-specific ORs for men and women are not meaningfully different in scenario B, the crude OR lies outside the stratum-specific ORs. Scenario B, therefore, demonstrates a situation where sex is a confounder in the association between smoking and CHD. In scenario C, the crude OR is closer to a weighted average of the two stratum-specific estimates (i.e., ORs). In other words, sex modifies the effect of smoking on CHD, i.e., sex is an effect modifier in the association between smoking and CHD. In the last scenario (D), the OR is again outside the stratum-specific ORs. However, unlike scenario B, the stratum-specific ORs appear to be different from each other. This might present a situation where sex is both confounder and effect modifier in the association between smoking and CHD.
To compare the stratum-specific effect estimates (ORs in this example), some investigators rely on comparison of the statistical significance of the effect estimates (i.e., p-values or 95% confidence intervals) across subgroups. This approach has been suggested to lead to erroneous claims about an effect modifier3. For instance, a statistically significant association in one subgroup (e.g., men), but not in the other (e.g., women) does not in itself provide evidence of effect modification. Direct evaluation of whether the magnitude of an association differs across the subgroups will result in a more valid inference and is the preferred approach3. Therefore, it is recommended to limit the statistical comparisons to reporting for statistical significance of the heterogeneity between subgroups using interaction terms5. Moreover, statistical comparisons should be corrected for the number of primary subgroup analyses performed5.
Stratified analysis can yield a full picture from the data that can be examined. However, for a detailed exploration, one might need to stratify the data by each of the factors and by various combinations of them. Therefore, the use of stratified analysis to identify possible sources of confounding or effect modification can become very complex, particularly in the situations where the sample size is small. Statistical modelling is another strategy that enables us to examine various relationships in detail. For example, a simple way to examine potential confounding by a variable is to fit two statistical models to the data, the first model including only the exposure and the outcome of interest and the second model additionally including the potential confounder. The next step is to compare the estimated measure of association between exposure and outcome of interest from the first and the second models, i.e., before and after adjusting for the potential confounder. If the difference between the two measures of association before and after adjustment is large enough, arbitrarily a change of 5%-10% or more, confounding is supposed to be present6. Multivariable statistical methods can also be used to assess the effect modification. To check for effect modification, an interaction term can be added to the statistical model. The interaction term is the product of “exposure of interest * potential effect modifier”. The multivariable statistical model will therefore be an equation relating the outcome of interest to the exposure of interest, potential effect modifier, as well as the product of the two (i.e., the interaction term). This statistical modelling will result in an interaction parameter, i.e., the effect estimate (or the coefficient), corresponding to the interaction term. If this interaction parameter is statistically significant, it indicates that the association between exposure of interest and outcome differs by the effect modifier (i.e., heterogeneity of effect). In statistical terms, this interaction coefficient is simply the difference of the slopes in the two subgroups defined by the potential effect modifier.
Reporting the results
Failure to detect and control for the important confounders or effect modifiers in the data can lead to erroneous inferences in interpreting the exposure-outcome associations in the study. The STrengthening the Reporting of OBservational studies in Epidemiology (STROBE) Statement guidelines require the investigators to define clearly all outcomes, exposures, predictors, potential confounders and effect modifiers in their study3. In case of confounding, the investigators are asked to clarify which confounders were adjusted for and why they were included. The guidelines also suggest reporting both unadjusted estimates and confounder-adjusted estimates together with their precision (e.g., 95% confidence interval). In the presence of effect measure modification, it is not appropriate to use statistical methods (e.g., Mantel-Haenszel) to combine the stratum-specific measures of association into a single pooled measurement. Effect modification is a biological phenomenon that should be properly described. Therefore, the stratum-specific estimates together with their precision need to be reported. In case of statistical modelling, the STROBE guidelines require the investigators to describe any methods used to examine subgroups and interactions. It is recommended to report the separate effects of each exposure as well as their joint effect to give the readers sufficient information to evaluate additive as well as multiplicative interaction. This will help the readers to understand how the joint effect of the exposure of interest and the effect modifier differs from their separate effects3.
Analysing sex in cardiovascular research
The proper investigation of confounding and effect modification should always be guided by the (biological) knowledge of the subject matter under study. The process of learning about and controlling for these two phenomena evolves gradually as we gain a deeper understanding of the underlying biology3. In cardiovascular research, sex has mainly been treated as a covariate and sex-specific analyses are often not adequately performed and reported. Our growing knowledge of sex-related differences in cardiovascular structure and function and in responses to various pathophysiological conditions and to treatment calls for re-evaluation of the current approaches used in the study of the cardiovascular system. As sex is a fundamental variable in all biomedical research, over and above consideration of sex as a confounder in the analysis, examining its potential role as an effect modifier in the association under study is of crucial importance7. A recent example is the significant interaction effect of sex in the Synergy between Percutaneous Coronary Intervention with TAXUS and Cardiac Surgery (SYNTAX) score II8. The SYNTAX score II is an important instrument for weighing anatomical and clinical factors that can assist clinicians in the decision-making process to establish the optimum revascularisation technique for individual patients with complex coronary artery disease. The SYNTAX score II was developed to overcome the limitations of its former version, i.e., the anatomical SYNTAX score, by further incorporating the clinical variables to allow a more individualised approach in clinical decision making. In development and validation of the SYNTAX score II, sex appeared to have a significant interaction effect, requiring lower anatomical SYNTAX scores for women to achieve similar long-term mortality after revascularisation8. Although the central role of sex in pathophysiology, prevention, treatment, and prognosis of cardiovascular disease is increasingly recognised, any evidence of statistical interaction should ideally be explained by an underlying biological mechanism. Interpretation of interaction effects should be cautious and viewed also in the context of additional prior/external evidence. As recommended by the PROGnosis RESearch Strategy (PROGRESS) 4 report, the identified interactions should be interpreted as hypothesis-generating, and replication in other studies as well as meta-analyses should be sought9.
Funding
Maryam Kavousi is supported by the VENI grant (91616079) from The Netherlands Organization for Health Research and Development (ZonMw).
Conflict of interest statement
The author has no conflicts of interest to declare.

