
In cardiovascular studies, it is common to assess the association between the risk of experiencing an event, such as death or hospitalisation, and one or more exposure variables, such as different treatment regimens when the study under consideration is an intervention study. A frequently applied measure of risk in such studies is the cumulative incidence, which is defined as the probability of experiencing the event of interest over some specified time period, such as one year. When all subjects remain under study until event occurrence, the cumulative incidence at a certain time point can readily be estimated by dividing the number of cases up to that time point by the number of subjects in the study population. Unfortunately, event times in clinical studies are often subjected to right censoring, which occurs when events are only observed if they happen prior to a censoring time that may vary from individual to individual1. In such situations, we can no longer estimate the cumulative incidence based on the sample proportions as we do not know how many of the subjects whose event time was censored should be counted as cases and how many as non-cases. We do know that these subjects were still event-free at the time of censoring: this is information that should be taken into account in the estimation of the cumulative incidence.
Right-censored observations can occur for several reasons2. First, in most clinical studies, there are subjects who are still event-free at the end of the study, resulting in right-censored event times at the end of the follow-up period. Second, it can happen that subjects withdraw from the study before the occurrence of the event of interest, resulting in censored observations at the time of study withdrawal. Finally, it may happen that another event has occurred which precludes the observation of the event of interest, resulting in censored event times at the time of occurrence of the competing event. This latter type of censoring, for example, occurs when one is interested in analysing the effect of treatment on cardiovascular-related mortality and some of the subjects die because of non-cardiovascular-related causes. Here, it is evident that the occurrence of non-cardiovascular-related mortality precludes the occurrence of cardiovascular-related mortality and, therefore, acts as a competing risk for the outcome of interest. Competing risks also occur when the primary study endpoint is a composite endpoint that combines fatal and non-fatal events, such as the major adverse cardiac events (MACE) endpoint, and interest centres around analysing the individual components of this combined endpoint. Here, it is clear that the fatal events preclude the non-fatal ones from occurring, meaning that we are again in the setting of competing risks when interest centres around the non-fatal events.
If censoring only occurs because of end of study or loss to follow-up, one can estimate the cumulative incidence of the event of interest at a certain time point by taking the complement (i.e., one minus) of the survival at the same time point, which can be estimated by applying “ordinary” survival analysis techniques, such as the Kaplan-Meier estimator. To illustrate how this works, Figure 1A shows the Kaplan-Meier survival curve for the all-cause mortality endpoint from the Coordinating study evaluating Outcomes of Advising and Counseling in Heart failure (COACH), a multicentre, randomised controlled trial in which 1,023 patients who were discharged alive from the hospital after having been admitted for reasons related to heart failure (HF) were followed for a maximum of 18 months3. This curve was produced by taking the time the individual died or was censored as the time variable and a dummy variable with the value 1 if the event was observed and 0 if the event was censored as the event indicator. The cumulative incidence curve that resulted from taking the complement of the Kaplan-Meier survival curve is shown in Figure 1B. From this curve, we can, for example, read that the one-year cumulative incidence of all-cause mortality in the COACH study was 0.203, with a 95% confidence interval (0.178, 0.228).
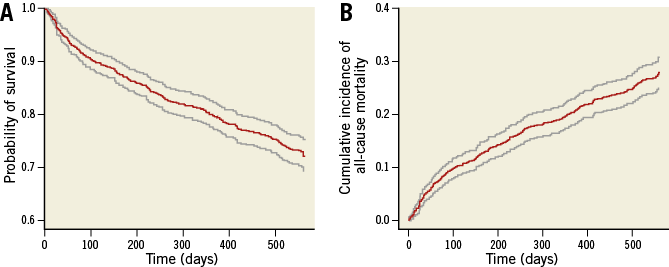
Figure 1. All-cause mortality in the COACH study. A) Survival curve. B) Cumulative incidence curve. The grey lines represent the 95% confidence intervals.
Now, consider the estimation of the cumulative incidence when there is censoring and subjects can fail from multiple event types. Technically, it is still possible to obtain Kaplan-Meier survival curves for each event type by treating the occurrence of a competing event as a censored observation. However, because the Kaplan-Meier estimator is based on the assumption that subjects who are event-free and under study are representative of those who were censored, these curves can no longer be interpreted as ordinary survival curves. Instead, they reflect the survival that would be observed in a world where all competing causes of failure have been completely eliminated2, which is lower than the survival in the real world, where subjects who experience a competing event are no longer at risk of the event of interest. In the presence of competing risks, the cumulative incidence of the event of interest will thus be lower compared to what is estimated by the one minus Kaplan-Meier estimator. This bias is illustrated in Figure 2 for the HF-related hospitalisation outcome of the COACH study, for which death occurring before hospitalisation acts as a competing risk. The dashed line represents the cumulative incidence curve that was obtained by using the one minus Kaplan-Meier estimator, and the solid line represents the true cumulative incidence curve, which was obtained using the non-parametric approach described in Putter et al2. It follows from the Figure that the true 18-month cumulative incidence of HF-related hospitalisation is 0.260, whereas the one minus Kaplan-Meier estimator yields an estimate of 0.284, resulting in a 2.4% overestimation of the event risk. The level of bias resulting from applying the one minus Kaplan-Meier estimator depends on both the total event rate and on how large the hazard of the competing event is compared to the hazard of the event of interest. This is demonstrated in Figure 3, where the true cumulative incidence curves and the ones obtained by using the one minus Kaplan-Meier estimator are depicted separately for the subset of patients with a B-type natriuretic peptide (BNP) value below (Figure 3A) or above (Figure 3B) the median of 447 pg/dL.
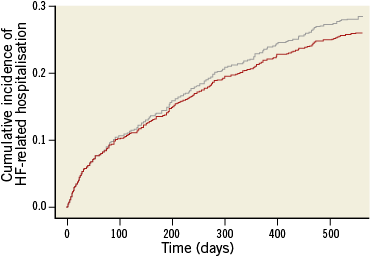
Figure 2. One minus Kaplan-Meier estimator (grey line) versus the true cumulative incidence curve (red line) for the HF-related hospitalisation outcome in the COACH study.

Figure 3. One minus Kaplan-Meier estimator (grey line) versus the true cumulative incidence curve (red line). A) Patients with a BNP value below the median of 447 pg/dL. B) Patients with a BNP value above the median of 447 pg/dL.
To conclude, although the one minus Kaplan-Meier estimator is frequently applied to estimate cumulative incidences in the presence of right censoring, this approach gives biased results when there are multiple event types and the occurrence of one of these event types precludes the event of interest from occurring. Given that the amount of bias gets larger as the number of subjects failing from a competing event increases, we suggest that the competing risks problem should be given special consideration, and appropriate statistical techniques applied, in the following settings in cardiovascular research: (i) studies dealing with a study population that is at higher risk of experiencing non-cardiovascular conditions, in addition to the cardiovascular diseases under investigation (e.g., cardiovascular studies involving a frail elderly population susceptible to non-cardiovascular comorbidities, such as cancer), (ii) studies with longer duration of follow-up, and (iii) studies with multiple potential event types (e.g., use of composite primary endpoints), especially when one is interested in the cumulative incidences of the individual event types.
Conflict of interest statement
The authors have no conflicts of interest to declare.

