In vivo validation of mathematically derived fractional flow reserve for assessing haemodynamics of coronary tandem lesions

Abstract

Aims: Our aim was to propose a prediction model for the post-stenting fractional flow reserve (FFR′d,pred) at a position distal to the tandem lesion.

Methods and results: Using the FFR at a position proximal to the tandem lesion (FFRp), and the FFR gradients across proximal (ΔFFRp) and distal (ΔFFRd) stenoses, FFR′d,pred after treating either the distal or proximal lesion was predicted as FFRp–ΔFFRp/(1-1.33kΔFFRd) or FFRp–ΔFFRd/(1-1.33ΔFFRp), respectively. The flow fraction of the distal main branch (k) was estimated using the diameter ratio of side to distal main branches. For in vivo validation, 50 patients with a tandem lesion (diameter stenosis >50%) were evaluated. Compared to the conventional model that did not consider side branch flow, our predicted FFR showed closer correlation with the measured FFR (R2=0.83 vs. 0.57) and significant reduction in mean absolute errors (0.034±0.028 vs. 0.053±0.049, p<0.001). In particular, with a large side branch and low baseline FFR, decision making using the current model had greater predictive ability than with the conventional model.

Conclusions: By predicting which stenosis is more severe and/or whether the remaining lesion after the first treatment is functionally significant, a tandem prediction model can help to plan optimised stent implantation.

Abbreviations

FFR: fractional flow reserve

PCI: percutaneous coronary intervention

QCA: quantitative coronary angiography

Introduction

Although lesion-specific fractional flow reserve (FFR) is a reliable index for assessing the haemodynamic significance of coronary artery stenosis1, a simple FFR measurement cannot predict the true functional severity of each individual stenosis in a tandem lesion (defined as serial stenoses within one coronary artery) due to mutual flow interaction between the stenoses2. In terms of optimal treatment sequence, previous studies have recommended that treatment of the stenosis with greater pressure or FFR gradient during pressure wire pullback should be prioritised. Therefore, because the functional severity of the remaining lesion can only be accurately assessed after treatment, a repeated FFR measurement is essential for further decision making3,4.

Previous studies using flow phantoms, animal models, and human patients5-7 have proposed theoretical equations for predicting the post-stenting FFR. However, these approaches were based on the assumption that there is no side branch between stenoses and that therefore there is a uniform flow rate across stenoses. Considering that the presence of a side branch significantly affects flow recovery after revascularisation and influences the distal pressure increase6,8, an approach that more accurately reflects coronary haemodynamic conditions is necessary. By predicting how many stents are needed and/or which stenosis is more severe, such an approach can help in the planning of optimised stent implantation and facilitate the stent procedure.

The aims of our present study were: 1) to develop and validate a mathematical model of tandem lesions to predict post-stenting FFR across the remaining stenosis, and 2) to propose a relevant approach for optimal treatment.

Methods

DEFINITION

FFR is defined as the ratio of mean coronary pressure to mean aortic pressure at maximal hyperaemia. The FFR gradient across an individual stenosis is represented as ΔFFR (ΔFFRp=FFRp−FFRm and ΔFFRd=FFRm−FFRd) (Figure 1). The primary target lesion was defined as the lesion with a larger ΔFFR between the proximal and distal stenoses. FFR (pre-procedure) and FFR′ (post-treatment of the primary target lesion) were obtained from initial and repeated pullback measurements, respectively.

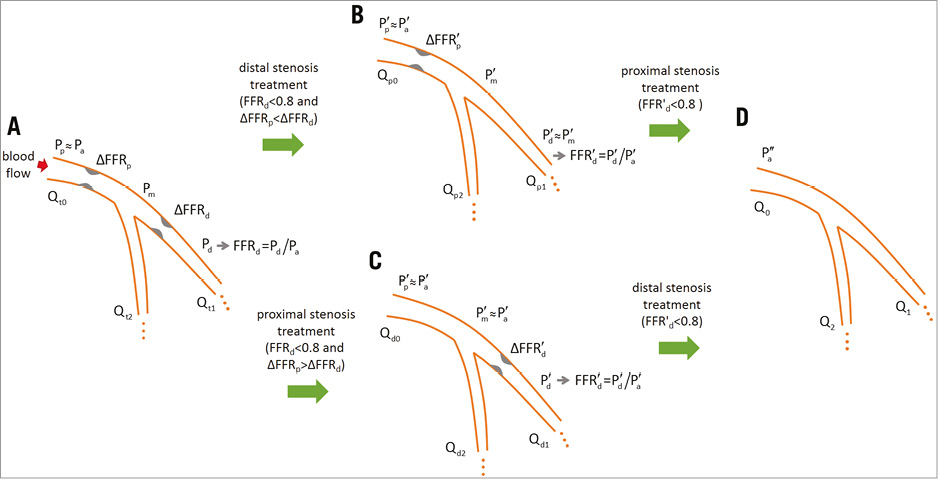
Figure 1. Changes in haemodynamic parameters after stenting. A) Before treatment. B) After distal treatment. C) After proximal treatment. D) After both treatments. Coronary flow rate (Q) is denoted by subscripts according to location (0, ostium; 1, main branch; 2, side branch) and lesion (d: distal; p: proximal; t: tandem). ′: after stenting a stenosis; ′′: after stenting both stenoses; FFR: fractional flow reserve; FFRp, FFRm, and FFRd: FFR values defined at the locations corresponding to Pp, Pm, and Pd, respectively; Pa: mean aortic pressure; Pp, Pm, and Pd: mean coronary pressures at positions proximal to the tandem lesion, between stenoses, and distal to the tandem lesion, respectively

DEVELOPMENT OF THE TANDEM PREDICTION MODEL

Figure 1A shows serial stenoses with an interposed side branch. Because the pressure gradient across normal lesions is negligible9, the distal pressures of the main and side branches are Pd and Pm, respectively. At maximum vasodilation, the flow rate to each branch is proportional to the difference between the distal pressure and the wedge pressure (Pw). By introducing resistances R1 and R2, the flow rates to the main and side branches are defined as

Qt1=(Pd−Pw)/R1 and Qt2=(Pm–Pw)/R2,

respectively. Pw is assumed to be the same for the main and side branches. After stenting the distal stenosis (Figure 1B), the distal pressure is changed to P′m. The flow rates to the main and side branches become

Qpl=(P′m−P′w)/R1 and Qp2=(P′m–P′w)/R2,

respectively, where P′w is the wedge pressure post stenting. Likewise, after treating the proximal stenosis (Figure 1C), the distal pressure is changed to P′d. Correspondingly, the flow rate to the main branch becomes

Qdl=(P′d−P′w)/R1.

To predict the FFR gradient across the proximal stenosis after stenting the distal stenosis, the linear relationship between the flow rate and the trans-stenotic pressure gradient is assumed as

By dividing with Pa/P′a and using the substitutions

Pd/Pa=1−ΔFFRp−ΔFFRd, Pm/Pa=1−ΔFFRp and P′m/P′a=1−ΔFFR′p,

(E1) .

For simplicity, we define two coefficients as

(E2) C1=(1/R1+1/R2)(1–Pw/Pa)=(1/R1+1/R2)(1–P′w/P′a) and C2=1/R1+1/R2.

For C1, the relationship between the aortic and wedge pressures is approximated as (Pw−Pv)/(Pa−Pv)≈Pw/Pa=constant, where Pv is the central venous pressure9. Using C1 and C2, equation (E1) is expressed as

.

By multiplying (C1−C2ΔFFR′p)/ΔFFRp,

.

By cancelling C2 and taking the inverse,

(E3) .

For the prediction of ΔFFR′d, the linear relationship between the flow rate and the pressure gradient across the distal stenosis yields

.

By dividing with Pa/P′a and using the substitutions

Pd/Pa=1−ΔFFRp−ΔFFRd and P′d/P′a=1−ΔFFR′d,

(E4) .

For simplicity, we define a coefficient as

C3=1–Pw/Pa=1–P′w/P′a,

and equation (E4) becomes

.

Rearrangement gives

,

and therefore

(E5) .

To estimate C1 and C2, the coronary bifurcation after stenting both stenoses is considered (Figure 1D). In ideal conditions, the distal pressure recovers to the mean aortic pressure (P′′a). Therefore, the flow rates to the main and side branches are

(E6) Q1=(P′′a–P′′w)/R1 and Q1=(P′′a–P′′w)/R2,

respectively. P′′w is the corresponding wedge pressure. Using the equation (E6), the term 1/R1+1/R2 in C1 can be expressed as

.

By substituting 1/R1+1/R2 into equation (E2),

By multiplying R1 and taking the inverse,

.

By defining w=1/C3=P′′a/(P′′a–P′′w)=Pa/(Pa–Pw) and k=Q1/Q0, equations (E3) and (E5) finally become

(E7) .

In the present study, Pw/Pa was assumed to be 0.256, and correspondingly w=1.33. The uncertainty associated with Pw was assessed by evaluating the variations in ΔFFR′p using the published standard deviation (Pw/Pa=0.25±0.10)6. The estimated error in FFR prediction was <0.02 for FFRd>0.6.

VALIDATION OF THE TANDEM PREDICTION MODEL

For tandem lesions, the distal FFR after the treatment of the distal or proximal stenosis is predicted as

,

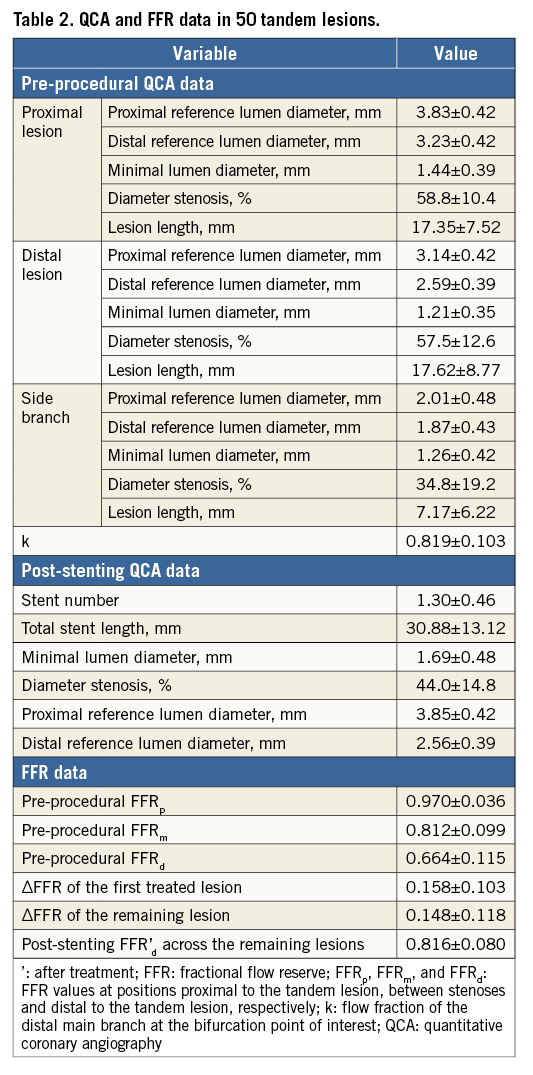
respectively (“current model”). k is the flow fraction of the distal main branch at the bifurcation point. To validate our mathematical models, the distal FFR measured after treating the primary target lesion (FFR′d) was compared with the predicted FFR value (FFR′d,pred). The baseline FFR values were calculated from the initial pullback measurement. k was estimated with the allometric scaling law of flow bifurcation10 using the diameters of coronary branches obtained by quantitative coronary angiography (QCA) (Figure 2). If multiple side branches were positioned in the tandem lesion, only the largest one was considered.

Figure 2. Plot of k vs. d2/d1. k: flow fraction of the distal main branch at the bifurcation point of interest; d2/d1: diameter ratio of side to distal main branches at the branching point (normal segment)

To compare prediction accuracy, predicted FFR values were computed by applying the “conventional model”,

,

for the treatment of proximal or distal stenosis, respectively5. The wedge pressure was estimated using the assumption of Pw/Pa=0.25, as in the current model.

STUDY SUBJECTS FOR MODEL VALIDATION

From November 2011 to May 2015, a total of 82 patients who had coronary tandem lesions with an FFR <0.80 at a position distal to the distal stenosis were retrospectively selected from the prospective FFR registry. A tandem lesion was defined as two separate stenoses within one epicardial coronary artery, each with a stenosis diameter >50% by visual estimation and separated by an angiographically normal segment. After excluding patients with acute coronary syndrome, significant left main coronary artery disease, incomplete stent coverage of the target lesion, coronary spasms, in-stent restenosis, left ventricular ejection fraction <40%, regional wall motion abnormalities, or coronary artery bypass grafts, 50 tandem lesions from 50 patients with complete angiographic and serial FFR data sets were analysed.

CORONARY ANGIOGRAPHIC AND FFR MEASUREMENT

Catheterisation was performed through the femoral or radial route using standard catheters. Coronary angiograms were digitally recorded and quantitatively assessed in the Angiographic Core Laboratory (Asan Medical Center, Seoul, South Korea), using an automated edge detection system (CAAS II; Pie Medical, Maastricht, The Netherlands). QCA analysis was conducted by experienced personnel according to standard clinical definitions11.

FFR measurements were performed using 0.014 inch pressure wires (St. Jude Medical, St. Paul, MN, USA) following standard procedures12. Under fluoroscopic guidance, the pressure wire was advanced into the coronary artery of interest to a position distal to the most distal stenosis, and steady-state maximum hyperaemia was induced by the continuous administration of 140-200 μm/kg/min adenosine into the large antecubital vein or the central vein. During maximal hyperaemia, the pressure wire was slowly pulled back to the ostium of the coronary artery while longitudinal pressure changes were recorded. The FFR values were automatically displayed, and all pressure tracings were recorded by a RadiAnalyzer™ Xpress (St. Jude Medical) for offline analysis. Finally, the pressure wire was completely pulled back into the guiding catheter to verify that no drift had occurred during the procedure.

After FFR measurement, percutaneous coronary intervention (PCI) for functionally significant tandem lesions (FFRd<0.80) was performed. First, a drug-eluting stent was implanted at the primary target lesion with the greater ΔFFR. Then, to assess the functional severity of the remaining stenosis, FFR′d was measured at the same position where FFRd was measured pre stenting. When FFR′d was <0.80, the remaining stenosis was treated by placing another stent. All procedures, including stent sizing and optimisation, were performed with intravascular ultrasound guidance.

STATISTICAL ANALYSIS

Continuous variables are presented as mean±SD, and categorical variables are presented as numbers and percentages. Linear regression analysis was performed to compare FFR′d,pred with FFR′d. Bland-Altman analysis was used to calculate the bias and limits of agreement between FFR′d,pred−FFR′d and FFR′d. To compare the prediction models, a paired t-test and Wilcoxon signed-rank test were applied to the prediction error (FFR′d,pred−FFR′d) and its absolute value (|FFR′d,pred−FFR′d|), respectively. Values of p<0.05 were considered statistically significant and normality of data was tested with the Shapiro-Wilk W-test (p>0.05). The Durbin-Watson statistic was calculated to test for a serial autocorrelation of the error terms in the regression models. All statistical analyses were performed using SPSS, Version 17.0 for Windows (SPSS, Inc., Chicago, IL, USA).

Results

PATIENTS

The baseline clinical, QCA, and FFR data in 50 patients with 50 tandem lesions are summarised in Table 1 and Table 2. The proximal stenosis was treated first in 27 (54%) patients, while the distal stenosis was treated first in the remaining 23 (46%) patients. In 37 (74%) patients, only a single stenosis was treated, with deferral of the remaining lesion.

PREDICTION ACCURACY COMPARED TO A CONVENTIONAL MODEL

The correlation between predicted and measured post-stenting FFR′ values and the accuracy of the prediction models are shown in Figure 3. The current prediction model (vs. conventional) showed a closer correlation with the measured FFR (R2=0.83 vs. 0.57). Correspondingly, our current model reduced the standard deviation of prediction errors by half (0.029±0.033 vs. 0.027±0.068, p=0.769) and had a greater prediction power in terms of absolute prediction errors (0.034±0.028 vs. 0.053±0.049, p<0.001). Also, in the ischaemia prediction of the remaining lesion (FFR′d<0.80), our current model yielded improved accuracy (82% vs. 78%).

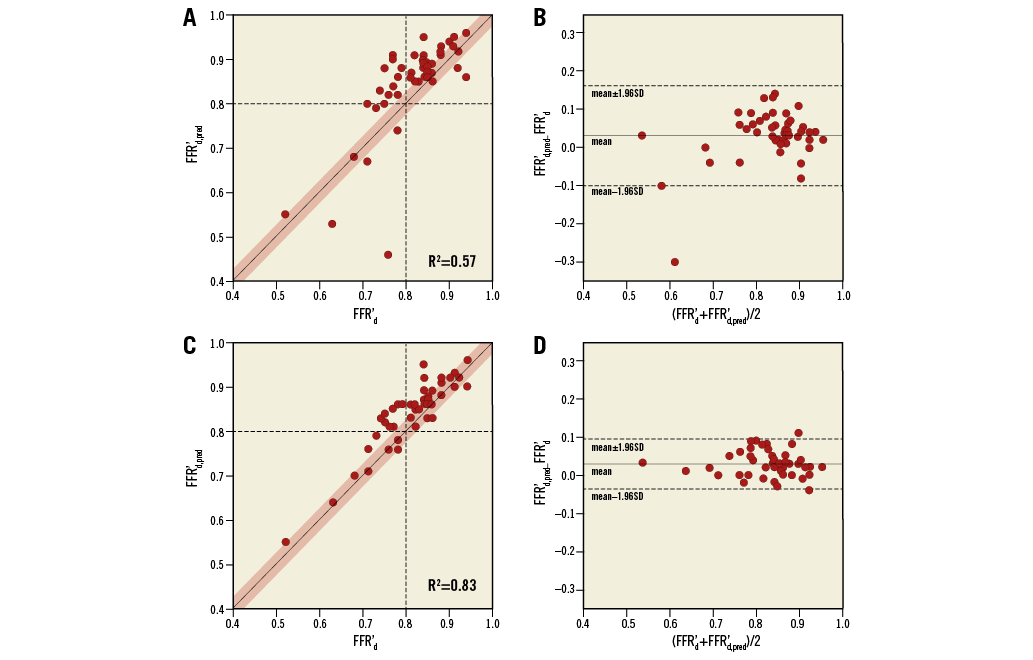
Figure 3. Plots of FFR′d,pred vs. FFR′d after stenosis treatment in a tandem lesion (left column) and the corresponding Bland-Altman plot (right column) for conventional (A, B) and current (C, D) models. For the current model, k is calculated using the diameter ratio of the side to distal main branches (Figure 2). Each dot indicates a tandem lesion. The red-shaded region in the left column indicates an offset of ±0.03. ′: after treatment; FFR: fractional flow reserve; FFRd: FFR at a position distal to the tandem lesion; pred: predicted

Decision making of tandem lesion treatment

DECISION DISAGREEMENT USING BASELINE ΔFFR VS. PREDICTED FFR’

The impact of side branch flow on the post-stenting FFR gradient is shown in Figure 4A, which was analytically obtained from the current prediction model. When ΔFFRp and ΔFFRd appeared to be equal, the post-stenting FFR′d,pred for the treatment of distal stenosis (vs. proximal) was higher, and the difference between post-stenting FFR′d,pred increased with lower FFRd and smaller k. Accordingly, disagreement in the decision making of the first target lesion using baseline ΔFFR and predicted post-stenting FFR′d,pred was observed, as shown in Figure 4B. When [ΔFFRd−ΔFFRp] was >0, the treatment of distal stenosis was predicted to be more effective in reducing ischaemia. Conversely, when [ΔFFRd−ΔFFRp] was <0, the distal stenosis could be more severe despite a larger ΔFFR across the proximal stenosis, as indicated by the “disagreement zone”. The lower the FFRd value and the higher the side branch flow, the larger the disagreement zone became.

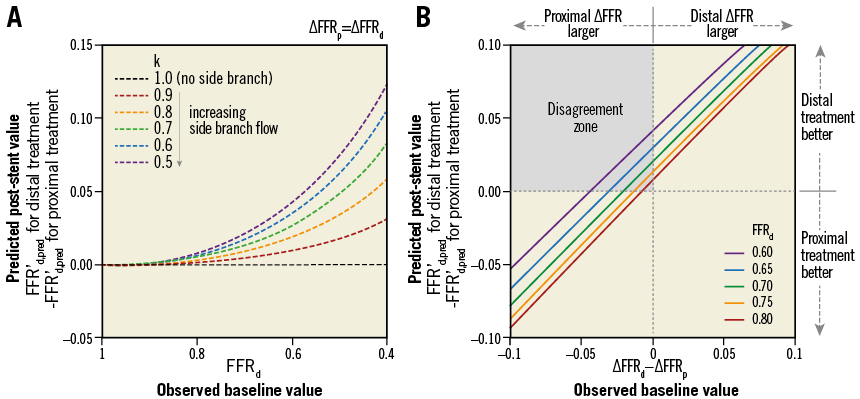
Figure 4. A disagreement in the decision making of the first target lesion using baseline ΔFFR and predicted post-stenting FFR′d,pred. When the baseline ΔFFRd and ΔFFRp are equal, the distal stenosis (vs. proximal) is predicted to be relatively more severe (higher FFR′d,pred for the treatment of distal stenosis) with a higher side branch flow (a smaller k) (A). When k is fixed as 0.5, the disagreement zone becomes larger with a lower baseline FFRd (B). ′: after treatment; FFR: fractional flow reserve; ΔFFR: translesional FFR gradient; FFRd: FFR at a position distal to the tandem lesion; ΔFFRp and ΔFFRd: FFR gradients across proximal and distal stenoses, respectively; k: flow fraction of the main branch at the bifurcation point of interest; pred: predicted

CASE EXAMPLE

The practical application of the current prediction model is explained in Figure 5. In the case example, the FFR value at the position proximal to the tandem lesion was FFRp=1, and the FFR gradients across the proximal and distal stenoses were ΔFFRp=0.23 and ΔFFRd=0.08, respectively. After the estimation of k (=0.66) using the diameter ratio of side to distal main branches (d2/d1=0.80), the FFR′d,pred was predicted to be 0.88 or 0.75 for the treatment of proximal or distal stenosis, respectively. The predicted FFR′d,pred indicated that the treatment of proximal stenosis was more effective and the treatment of distal stenosis was not necessary. For this patient, only the proximal stenosis was treated, and the measured post-stenting FFR′d was 0.85.

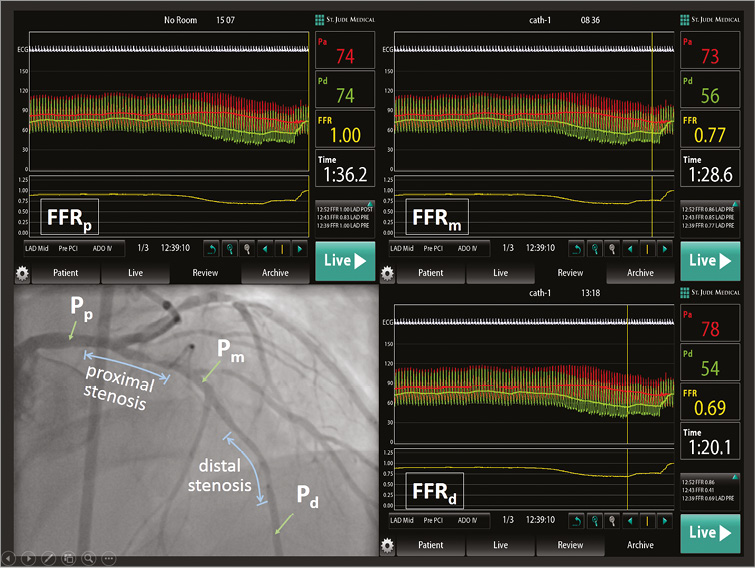
Figure 5. Case example of the use of the current prediction model to assess a tandem lesion. Using the baseline FFR gradients (ΔFFRp=0.23 and ΔFFRd=0.08) and the estimated k (=0.66), the post-stenting FFR′d,pred was predicted to be 0.88 or 0.75 for the treatment of proximal or distal stenosis, respectively. After treating the proximal stenosis, the measured post-stenting FFR′d was 0.85. FFR at a position proximal to the tandem lesion. FFR: fractional flow reserve; FFR′d: FFR distal to the tandem lesion after treatment; ΔFFRp and ΔFFRd: FFR gradients across proximal and distal stenoses, respectively; k: flow fraction of the distal main branch at the bifurcation point of interest; pred: predicted; QCA: quantitative coronary angiography

UTILISATION OF A ΔFFR MAP

To facilitate clinical decision making, optimal treatment strategies for tandem lesions were suggested by the ∆FFR map based on the current prediction model in which the baseline distal FFR was functionally significant (FFRd<0.80) (Figure 6). The ΔFFR map was divided into three sub-regions by a red line (the same FFR′d,pred for the treatment of proximal and distal stenoses), blue line (FFR′d,pred=0.8 for the treatment of distal stenosis) and green line (FFR′d,pred=0.8 for the treatment of proximal stenosis). Accordingly, tandem lesions were categorised into “treat only distal”, “treat only proximal” and “treat both”. Depending on the side branch flow, the boundaries of “treat only distal” (red and blue lines) were modified, while the green line remained constant. Therefore, evaluation and comparison of FFR′d,pred using the current prediction model were required in the blue area to determine whether only the distal lesion or both lesions should be treated, as well as in the orange area to decide whether the distal or proximal lesion should be treated. For the patient shown in Figure 5, the baseline FFR gradients (∆FFRp=0.23 and ∆FFRd=0.09) indicated that only the proximal lesion should be treated.

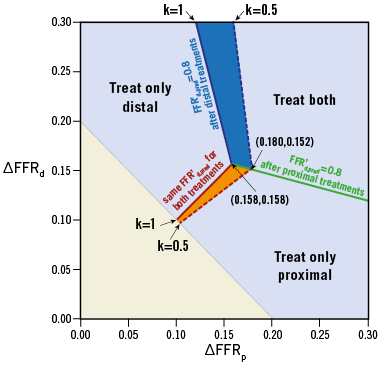
Figure 6. ΔFFR map for clinical decision making in tandem lesions. The evaluation and comparison of post-stenting FFR′d,pred using the current prediction model are required in the blue and orange areas, where the boundaries are dependent on k; otherwise, the decision can be directly made. Here, FFRp=1 is assumed, and, for the patients with FFRp=1, the prediction accuracy of this map was 91% (20/22). ′: after treatment; FFR: fractional flow reserve; ΔFFR: translesional FFR gradient; ΔFFRp and ΔFFRd: FFR gradients across proximal and distal stenoses, respectively; k: flow fraction of the distal main branch at the bifurcation point of interest

Discussion

While FFR is reliable for assessing the haemodynamic significance of coronary artery stenosis, the functional severity of individual stenoses cannot be assessed without repeated FFR measurements in tandem lesions with an interposed side branch. Therefore, the aim of our present study was to provide and validate a mathematical prediction model for post-stenting FFR′d,pred. The major findings of our present study were: 1) a mathematical prediction model reflecting the actual severity of individual stenoses and the effect of interposed side branches allowed us to predict post-stenting FFR′ accurately across the remaining stenosis (R2=0.83 between predicted vs. measured FFR′); and 2) this prediction model was helpful in deciding which stenosis was more severe and whether the remaining lesion after the first treatment was functionally significant.

Our current results showed an improvement in accuracy using the current prediction model. This may be explained by three factors. First, the effect of interposed side branches was considered in the current model. Although the conventional model achieved high prediction accuracy for tandem lesions with negligible side branches6, larger discrepancies were observed in the population with various sizes of side branch. Second, the conventional prediction model overestimated the ΔFFRp by ignoring the pressure drop from the coronary ostium to the tandem lesion (FFRp≠1). In 27 tandem lesions, including 22 left anterior descending arteries, consideration of FFRp (0.947±0.032) improved the accuracy of our prediction model, although further evaluation of dynamic changes in FFR′p post stenting is needed to clarify this issue7. Third, the FFR-based (not pressure-based) calculation in our prediction model was amenable to variations in aortic pressure during the pullback measurement, independently of blood pressure13.

The measurement of wedge pressure (Pw) is considered a main obstacle to the clinical use of prediction models6,12, and, in tandem lesions, direct measurements for both side and distal main branches are virtually impossible. In our current model, the need for wedge pressure information was eliminated with the assumption of Pw/Pa=0.25. The prediction error of using the fixed Pw/Pa was demonstrated to be within the clinically acceptable range (<0.02 when FFRd >0.6). The flow bifurcation ratio (k) was also estimated without direct measurements. The plot of k vs. d2/d1 shown in Figure 2 can be simply used for the estimation of k, and, for tandem lesions with no side branch, post-stenting FFR prediction can be achieved by applying k=1. Considering the prediction error associated with k estimation (≤0.01 per 0.1 of k when FFRd >0.6 in Figure 4A), the k value obtained with a rough estimation of the diameter ratio did not hamper the prediction accuracy, and therefore the real-time application of the current model would be feasible in a clinical context. Moreover, the ΔFFR map that was provided based on the current prediction model facilitates immediate decision making for the optimal treatment strategy for tandem lesions. Consequently, the current model is more customised to the clinical context, allowing us to predict post-stenting FFR′ accurately without wedge pressure measurements.

A recent study reported that the FFR gradient (ΔFFR) was theoretically the same as the pressure gradient across a stenosis, but was a more feasible and practical index for comparing the relative functional severity between two separate lesions3. Thus, it has been recommended that the stenosis with the larger ΔFFR should be treated first, and that the post-stenting FFR′d across the remaining stenosis should then be evaluated. However, our prediction model showed that there was a disagreement zone in which the decision making for more effective treatment was different between the evaluation of the baseline ΔFFR and the predicted post-stenting FFR′d,pred. With the flow-dependent property of pressure gradients, proximal and distal stenoses mutually affect each ΔFFR. If there is no side branch between two separate lesions, the baseline ΔFFR values equally underestimate the true severities of both stenoses, and thus reveal which stenosis is more severe. However, because an increase in side branch flow attenuates the recovery of the coronary flow across the proximal stenosis after the treatment of the distal stenosis and not vice versa, equal baseline ΔFFR values imply that the distal stenosis is more severe. In the same context, the interpretation of our current model is consistent with the recent reports that stenting a downstream stenosis produced little change in the FFR gradient across the intermediate left main disease14,15, because the treatment of a stenosis in the left anterior descending or left circumflex restores a fraction of the flow rate running through the left main. Nonetheless, for the FFR prediction of tandem lesions with left main diseases, further investigations should be made. These findings suggest that treatment of the proximal stenosis with a larger ΔFFR could be less effective, particularly with more severe lesions and higher side branch flow.

Furthermore, our current prediction model, unlike the simple comparison of baseline ΔFFR values, makes it possible to simulate the residual FFR after the first treatment and thus to plan for a tailored stent before the procedure. For instance, there may be technical difficulties in delivering the second stent to the distal site through the primarily stented proximal segment. If the presence of residual ischaemia is predicted and both stenoses should be treated, operators can avoid unnecessarily complex procedures by first treating the distal lesion.

Limitations

Our current study had some potential limitations. First, the small sample size and potential selection bias may have affected the results. Second, the linear relationship between the cycle-averaged pressure and flow rate could ignore the transient characteristics of coronary flows, and did not include the quadratic term associated with flow separation and turbulence around the stenosis, which may have caused an additional pressure drop16,17. Third, the wedge pressures for the distal main and side branches were assumed to be equal. Fourth, our current model did not include the assessment of left main lesions with downstream stenoses and cannot be applied to lesions with more than two stenoses, multiple large side branches, or diffuse lesions. Fifth, the outcome of FFR prediction could be impaired when distal embolisation occurs as a consequence of extensive vessel manipulation or degree of platelet inhibition. Sixth, the bifurcation angle was not considered in the calculation, which could be an important determinant for the flow fraction to branches18. Finally, despite our efforts to apply the prediction model simply in daily practice, its clinical relevancy needs to be further validated with subsequent clinical studies.

Conclusion

Post-stenting FFR in tandem lesions with an interposed side branch can be accurately predicted without the measurement of wedge pressure. By predicting which stenosis is more severe and/or whether the remaining lesion after the first treatment is functionally significant, this tandem prediction model can help in planning optimised stent implantation and facilitate the stent procedure.

Funding

This study was supported by a grant from the Korea Healthcare Technology R&D Project, Ministry for Health & Welfare Affairs, Republic of Korea (HI14C0517 and HI12C0630), a National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIP) (NRF-2015R1A2A2A04003034), and by the Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Science, ICT & Future Planning (NRF-2013R1A1A1058711).

Conflict of interest statement

The authors have no conflicts of interest to declare.