
We appreciate the interest in our article1. The author raised the issues of the driving force for myocardial flow, the flow ratio estimation, and the procedural order. Also, the author suggested that the application of the prediction model in Yaeger2 would improve the outcomes of FFR prediction.
Spaan et al3 showed that, even without collateral flows, (Pd–Pv)/(Pa–Pv) overestimates the coronary flow ratio (QS/QN) and the microvascular resistance (Rmin) increases as the distal pressure (Pd) falls. To build an equation to describe the P–Q relationship better, we introduced “R” corresponding to the inverse of the slope for Q vs. Pd–Pw, instead of using a constant microvascular resistance (Figure4 in Spaan et al3). The flow ratios to branches, in the same regard, were estimated using anatomical metrics. Because “R” in our mathematical derivation is dimensionally equivalent to the resistance in electronic circuit modelling, we called it “resistance”.
For determining the procedural order, previous studies have recommended that treatment of the stenosis with greater pressure or FFR gradient during pressure wire pullback should be prioritised4, as addressed in the introduction of our article1. Please remember that the objective of our work was to propose a better method for predicting more severe lesions.
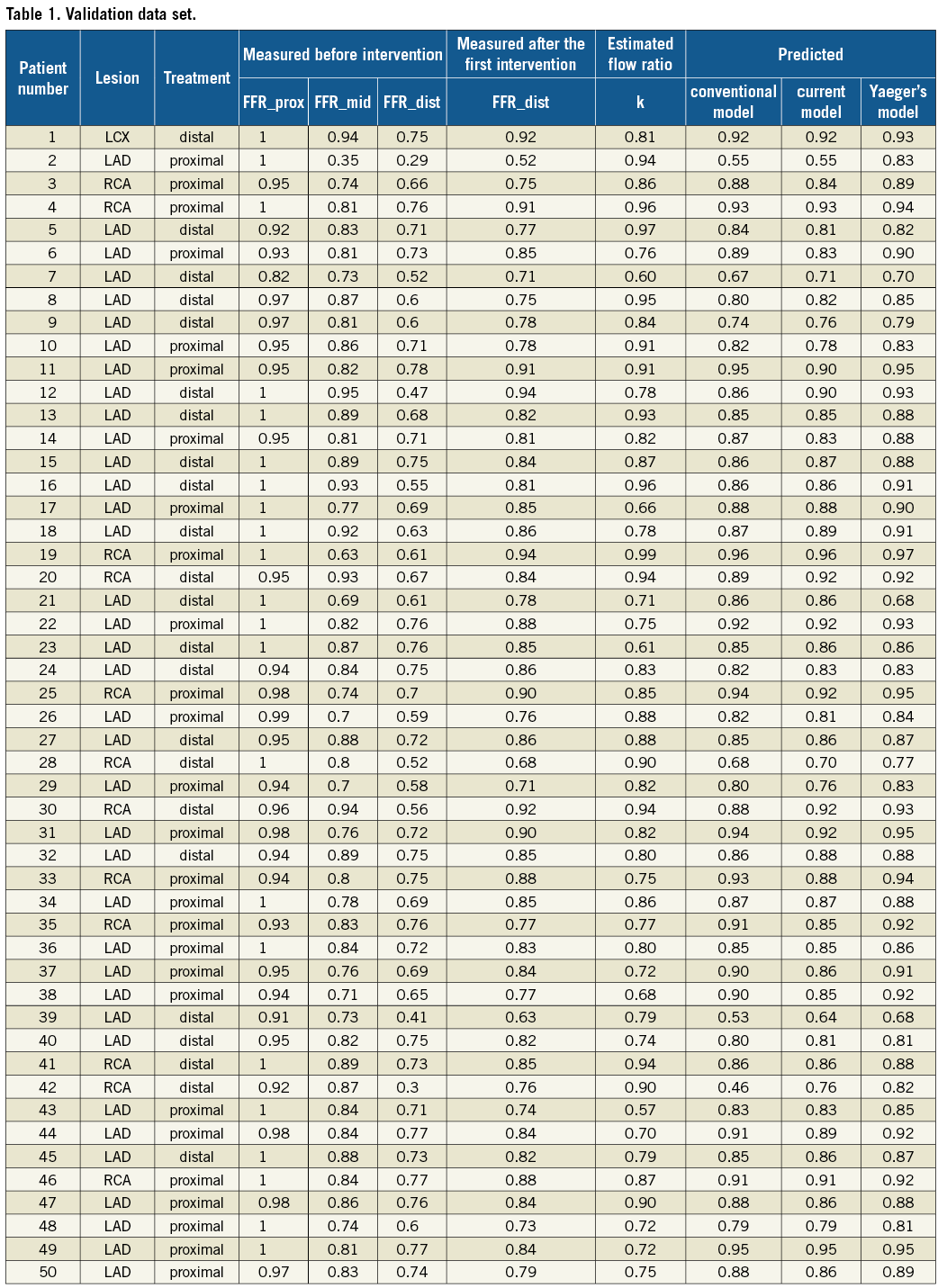
The prediction model of Yaeger2 was examined and the outcomes are listed in Table 1. The mean error was 0.057±0.059 and the mean absolute error was 0.063±0.052. In the Appendix, please find the translation of Yaeger’s prediction model2 to the notations in our derivation.
Appendix. Translation of Yaeger’s prediction model to the notations in the derivation by Kweon et al
For simplicity, abbreviations are used as follows.
FFRapp(LM)=a
FFRtrue(LM)=b
FFRapp(LAD) =FFRtrue(LAD)=c Eq (*1)
FFRreal(LM)=d
FFRreal(LAD)=e
From the pullback measurement, FFRapp(LM) and FFRapp(LAD) are obtained. For the comparison with our mathematical model, we rephrased the equations in Yaeger2 as functions of “a” and “c” as follows.
Equation (19) in Yaeger2 is:
![]()
Using the abbreviations above, it becomes:
![]() Eq (*2)
Eq (*2)
By multiplying both numerator and denominator by 2b, we can get:
![]() .
.
By multiplying both sides by the denominator, it becomes:
a(1+b+c–bc)=2b and a(1+c)=b(ac–a+2).
Subsequently, b can be expressed as:
![]() . Eq (*3)
. Eq (*3)
Equation (23) in Yaeger2 is:
![]() .
.
Using the abbreviations above, it becomes:
![]() .
.
Using the expression in Eq (*3), we can get:
![]() .
.
Using the notations in Yaeger2, the prediction equation for LAD treatment becomes:
![]() .
.
Equation (34) for the LM treatment in Yaeger2 is:
![]() .
.
Using the abbreviations above, it becomes:
![]() .
.
Using the expression in Eq (*2), we can get:
e=ac.
Using the notations in Yaeger2, the prediction equation for LM treatment becomes:
FFRreal (LAD)=FFRapp (LM)×FFRtrue (LAD).
Using the notations in our derivation, the equations above are translated as follows:
![]() for proximal treatment,
for proximal treatment,
![]() for distal treatment.
for distal treatment.
Conflict of interest statement
The authors have no conflicts of interest to declare.
Supplementary data
Both of the letters to the Editor disputing the paper, “Invivo validation of mathematically derived fractional flow reserve for assessing haemodynamics of coronary tandem lesions”1, together with all further correspondence can be found online in the Supplementary data.
To read the full content of this article, please download the PDF.

