The ACEF score: basic principles
In 2009, our group published a study proposing the use of only three factors for assessing the operative mortality risk in elective cardiac operations1. The three factors included in the model are age (as a continuous variable), left ventricular ejection fraction (EF, continuous variable) and preoperative serum creatinine value (binary value), constituting the ACEF score (an acronym of: age, creatinine and EF). The calculations required for assessing the ACEF score are quite simple: age (years)/ejection fraction (%) plus one additional point if the preoperative serum creatinine value is ≥2.0 mg/dL. According to the ACEF score, the operative mortality risk may be assessed by solving the equation:
Mortality risk=eACEFscorex1.24–5.41 / (1+ eACEFscore x 1.24–5.41)
or simply using the graphical relationship reported in Figure 1.
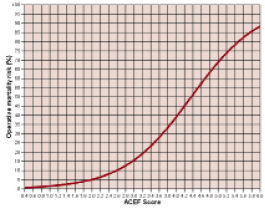
Figure 1. Predicted mortality rate in adult elective patients undergoing cardiac operations according to the ACEF score.
In an internal validation series, the ACEF score had an accuracy similar to the other existing risk scores with an area under the curve or c-statistics of 0.81 at the receiver operating characteristics analysis. The clinical performance was better using the ACEF score than using either the additive or the logistic EuroSCORE1.
The ACEF score is based on the “law of parsimony” or the “Occam’s razor” concept, and tends to exclude some of the confounders that could bias the other existing scores, which include many more variables. Basically, these biases pertain to different domains.
Risk factor definitions
The three risk factors used in the ACEF score are natural continuous variables.
One (age) is definitely not subject to personal estimation. Serum creatinine may have different values reported in the patient’s files; in this case, the most recent measure should be considered. The third factor (ejection fraction) could be less defined since the patient may reach the operating room with different values reported in different examinations (angiography or echocardiography) or even within the same kind of examination done at different times. Again, in case of multiple determinations, the ACEF considers the most recently measured EF value or the lowest value of EF in cases where multiple values are available immediately before the operation. Of course, the main problem is in the case of a missing EF value, since this makes the ACEF score calculation impossible. However, missing the EF value very rarely (<1% in our series) occurs, and usually this happens in cases of emergency operations, that are excluded by the ACEF score.
So, by following this simple approach, the ACEF calculation is not subject to personal interpretation.
Including other factors (“comorbidities”) within a risk score (as done by all the other available risk models) may theoretically increase the accuracy of the model. However, a strict definition for each comorbid condition is needed. This applies to chronic obstructive pulmonary disease, cerebrovascular disease, extracardiac arteriopathy, unstable angina and others. Of course, each of the existing risk scores is equipped with a set of “definitions” which should guide those who calculate the score, avoiding personal interpretations. But in the real world, things do not necessarily follow this virtuous direction. The same patient, evaluated by different care providers (anaesthesiologists, cardiologists, cardiac surgeons) may come out with different risk assessments whenever their clinical judgement is involved in the adjudication of a comorbidity. For example, the Cardiac Anaesthesia Risk Evaluation (CARE) score is a very simple tool which grades the surgical risk into five categories by taking into account the clinical judgement for comorbid conditions (controlled or uncontrolled)2. It has an accuracy comparable to the EuroSCORE3, but an intra-observer agreement which may be of only 77% (anaesthesiologists vs. cardiologists)3. This intra-observer variability may be seen even as an intra-institutional variability. Recently, a wide (more than 32,000 patients) Italian study on coronary artery bypass graft (CABG) operations4, where the operative mortality was adjusted for the EuroSCORE, revealed a huge intra-institution variability in the definition of many risk factors, with a mean rate of unstable angina of 24%, but with institutions reporting this condition at rates ranging from 15% to 62%, and a mean rate of cardiogenic shock of 1%, but with institutions reporting up to a 7% rate. Same wide variations were observed for chronic obstructive pulmonary disease and diabetes, and due to this and other reasons the study was greatly criticised5 and actually not endorsed by the Italian Society of Cardiac Surgery.
The more conditions subjected to clinical judgement are included in a risk model, the more this model will suffer from inter-individual and inter-institution variability.
Binary and continuous variables
Dichotomising or categorising natural continuous variables is always a difficult task. It is understandable that for practical reasons this has been done for age, left ventricular EF and serum creatinine in the existing risk scores (Parsonnet, Cleveland Clinic, EuroSCORE, and others). However, this is often arbitrary in an era when we frequently operate on patients aged 80 years or more, and who have a left ventricular EF of 20% or less. The existing scores (before the ACEF) did not discriminate between these very poor EF values, simply categorising them in a field below 30% (Parsonnet score and EuroSCORE), 35% (Cleveland Clinic score) or 40%. In the ACEF score, the crucial importance of EF is highlighted by including this risk factor as a continuous variable, with every possible value included in the final score. The same applies to age, which again is used as a natural continuous variable in the ACEF score.
Serum creatinine is dichotomised in the ACEF score as in the previous scores for preserving the philosophy of an easy and fast calculation – and not by chance this was criticised6. We must admit that this criticism is reasonable and that the ACEF score is probably improvable, in this respect7.
The risk related to the operation
The ACEF score was built for elective cases and has not been validated in urgent/emergent procedures. This may be a limitation, but again this avoids misinterpretations of the urgent or emergent nature of the operation.
Most importantly, the ACEF score does not include any detail about the type of cardiac operation (isolated CABG, isolated valve, combined procedures, etc.).
Is it possible to build a risk model which does not take into account the type of operation? Apparently, this approach should generate a great bias, pooling together operations at very low risk (isolated CABG, isolated aortic valve replacement) and operations at very high risk (CABG plus mitral valve repair/replacement; double or triple valve operations, etc.). However, if we look at how this problem was addressed by the other risk models, we could even conclude that no classification of the operation-related risk is better than a bad classification.
Whereas the Cleveland Clinic8 and the Northern New England9 scores are limited to CABG operations, the widely used EuroSCORE10 attributes a specific risk score only to ascending aorta operations and post myocardial infarction ventricular septum repair. All other operations are simply defined as “non-isolated CABG”; therefore, this risk score attributes the same risk to an isolated aortic valve replacement and a CABG plus mitral valve procedure or a double/triple valve procedure, even if it is well known that the mortality risk of the two last operations is double or triple that of an isolated CABG operation.
Probably, the only reasonable way to address the problem of the operation-related risk is providing different, parallel risk models for each major operation (or group of operations). This approach is followed by the STS-PROM, even if available in a limited subset of operations.
ACEF score: the present, and the future
The ACEF score was developed and validated in the same institution. Therefore, an external validation is needed. A large multicentre Italian study including more than 19,000 elective patients has been recently closed. This study compares the observed operative mortality rate with the predicted mortality rates obtained using the ACEF score and the EuroSCORE. The results of the study were presented at the last meeting of the European Society of Cardiology, which took place in Stockholm, Sweden in August-September 2010.
An interesting attempt to apply the ACEF score to different settings of patients has been recently proposed11. Garg and coworkers12 merged the SYNTAX angiographic lesion severity score into a modified ACEF score for addressing the risk of: i) major adverse cardiac or cerebrovascular events (MACCE – death, myocardial infarction, stroke and repeat revascularisation) and ii) mortality after one and five years from a percutaneous coronary intervention. The modified ACEF score includes the serum creatinine clearance instead of the serum creatinine as a risk factor and attributes 1 point for each 10 ml of creatinine clearance reduction below 60 ml/min/1.73 m2.11,12
The clinical SYNTAX score is simply:
SYNTAX score × Modified ACEF score
Garg and coworkers12 could demonstrate that the clinical SYNTAX score is superior to either the SYNTAX score or the ACEF score in predicting MACCE and mortality, and that combining the SYNTAX score with the more detailed EuroSCORE did not increase the accuracy of the prediction as obtained with the clinical SYNTAX score.
We very much appreciate this approach that actually could overcome the limitation of considering the serum creatinine value as a binary variable. We agree that preoperative renal dysfunction is a mortality risk factor even in a range lower than 2.0 mg/dL6, and the use of creatinine clearance as a semi-continuous variable may probably increase the accuracy of the model.
We tested the modified ACEF score in the same series of 4,091 patients used for validation of the ACEF score1) and obtained a slight increase in the accuracy of prediction with a c-statistics increase from 0.808 to 0.813 (Figure 2). Interestingly, the modified ACEF score performed better in the non-coronary patients series (N=1,019), with a c-statistics of 0.869 vs. 0.848 for the ACEF score (Figure 2).
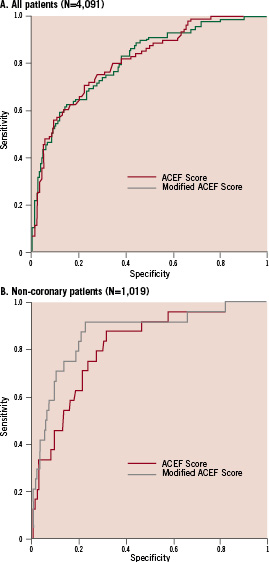
Figure 2. Receiver operating curves for the ACEF score and modified ACEF score in cardiac surgical patients (A) and in the subgroup of non-coronary patients (B).
It should, however, be considered that when the serum creatinine clearance is calculated according to the Cockcroft-Gault equation we are probably introducing a mathematical coupling and a co-linearity bias into the ACEF risk model. As a matter of fact, age is counted twice, first alone, and secondly within the Cockcroft-Gault equation. However, even if not totally correct from a pure statistical point of view, this correction of the ACEF opens promising scenarios.
The ACEF score has been tested in comparison with the EuroSCORE as a tool for risk stratification in patients with severe aortic valve stenosis to be referred for transcatheter aortic valve implantation (TAVI)13. In a population of 1,264 patients (1,053 surgical procedures and 211 TAVI), the EuroSCORE and the ACEF score had a similar level of accuracy, with a better calibration for the ACEF score. For the definition of patients at very high operative mortality risk (>10%), this value corresponds to a EuroSCORE of 26 and an ACEF score of 2.5.
When we first proposed the ACEF score for operative risk stratification in elective cardiac surgery it was not our intention to replace the existing risk scores with this very simple tool. Our conclusions were that “the equivalence... [between the EuroSCORE and the ACEF score]...could be seen in terms of two well performing models as well as two bad performing models”1. What we are today facing is a possible different use of the ACEF score.
It is reasonable to hypothesise that age, renal function and left ventricle performance may be independent risk factors for mortality in many different clinical conditions (and actually, even in daily life, elderly people with poor left ventricular ejection fraction and renal dysfunction are at high risk of an early death). The example of the clinical SYNTAX score applied to percutaneous coronary procedures is a nice way for using the ACEF score as a clinical basis on which to build specific risk models for specific conditions. In the case of the clinical SYNTAX score, the ACEF acts as a clinical adjustment factor for the coronary lesion severity (at the end of the day, coronary vessels are placed into a human being).
In other cases, different approaches could be applied. For example, the ACEF score could be a simple basis for risk stratification and selection of patients for TAVI procedures, providing that we can merge into the ACEF score many different possible “extreme” risk conditions (chronic obstructive pulmonary disease under oxygen treatment, hepatic cirrhosis, hostile chest, etc.).
The strategy of a two step approach for risk stratification (first step, a simple generic clinical model like the ACEF score; second step, multiply for a specific risk condition or specific risk score) may offer some advantages. Actually, the usual approach for risk models, based on multivariable logistic regression analyses, does not allow including in the models many very rare conditions which yield a very high mortality risk. These conditions are certainly associated with the operative mortality risk at the univariate analysis, with extremely high values of odds ratio; however, they almost invariably disappear as independent risk factors at the multivariable analysis, when they have a very low prevalence (<0.2%). For example, this is the case of severe preoperative liver failure.
In a recent analysis of our database, which includes more than 13,000 adult cardiac patients operated at our institution, we could identify this condition in 0.1% of the patients, with an odds ratio for operative mortality of 4.2 (95% confidence interval 1.1–19). A significant four-fold increase in mortality risk totally disappears as an independent variable for operative mortality if we include it together with the other covariates in a stepwise forward multivariable logistic regression model.
However, in the same series, the ACEF score yields a c-statistic of 0.767 for prediction of operative mortality, which raises to 0.771 by simply multiplying it by four in case of severe chronic liver failure.
In conclusion, we think that the attempts of incorporating the ACEF score into existing models created for stratifying the risk of other procedures deserves great attention. Actually, when we proposed the ACEF score as a simple tool for predicting operative mortality in elective patients undergoing cardiac surgery, we were well aware of the limitations of this model. However, it is our opinion that the same limitations apply to all the other more complex existing models, which carry the burden of subjective definitions, co-linearity between the risk factors, and need for many more data and calculations.
Risk models help clinicians in their clinical work, but looking for the “ultimate” risk score, with sensitivity and specificity close to 100% is probably more an illusion than a reasonable goal.
It is our opinion that the ACEF should be considered as a skeleton waiting for muscles, skin, and internal organs. Starting with this simple risk stratification, different variables may be added depending on the procedure whose risk we want to estimate. This, of course, should be done without losing the simple and parsimonious concept of the ACEF score. We therefore acknowledge great merit to these attempts for improving the risk stratification in different cardiovascular procedures, and we think that the Clinical SYNTAX score may represent a novel and promising approach in this direction.

