Abstract
Aims: The percutaneous repair of a diseased segment should consider the dimensions of other segments of a bifurcation in order to ensure the optimality of flow through the bifurcation. The question is, if the diameters of two segments of a bifurcation are known, can an optimal diameter of the third diseased segment be determined such that the bifurcation has an optimal geometry for flow transport? Various models (i.e., Murray, Finet, area-preservation and HK models) that express a diameter relationship of the three segments of a bifurcation have been proposed to answer the question.
Methods and results: In this study the four models were compared with experimental measurements on epicardial coronary bifurcations of patients and swine. The HK model is found to be in agreement with morphometric measurements of all bifurcation types and is based on the minimum energy hypothesis while Murray and area-preservation models are in agreement with experimental measurements for bifurcations with daughter diameter ratio (i.e., small daughter diameter/large daughter diameter) ≤0.25 and Finet model is in agreement for bifurcations with daughter diameter ratio ≥0.75.
Conclusions: The HK model provides a comprehensive rule for the percutaneous reconstruction of the diameters of diseased vessels and has a physical basis.
Introduction
Percutaneous coronary intervention (PCI) attempts to restore the lumen area of a diseased artery to “normal” reference dimension through percutaneous transluminal coronary angioplasty (PTCA) or stenting. As atherosclerosis often stems from the junction of a bifurcation1 and diffuses over the vessel length8,12,13, the question becomes what is the therapeutic target diameter of the diseased vessel to restore flow optimality to a bifurcation. In other words, if the diameters of two segments of a “normal” bifurcation are known, can an optimal diameter of the third segment be determined to ensure an optimal flow through the bifurcation?
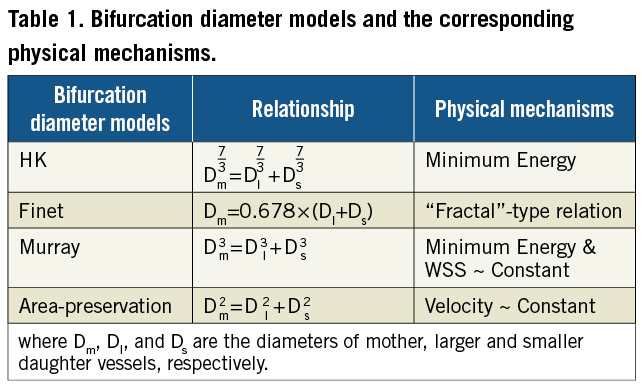
It has long been established that there is an optimal relationship between the diameters of the three segments of a bifurcation. Table 1 lists the most commonly referenced bifurcation models that provide a mathematical relationship between the three segments of a bifurcation (i.e., Dm, Dl and Ds for the diameters of mother, large and small daughters, respectively). In 1926, Murray was the first to derive a cubed relationship between the mother and two daughter vessels11. The premise of Murray’s derivation is the minimum energy hypothesis; i.e., the power for transport of blood through a bifurcation is minimised. This is the principle of efficiency where departure from which requires greater energy dissipation. Huo and Kassab7 recently showed a similar relationship based on the same premise in a tree structure, but found an exponent of 7/3 instead of 3 in the Murray model. Finet et al3 proposed an empirical fractal-like rule. An additional expression stemming from area conservation (exponent of 2) has traditionally been invoked for the vasculature9.
The objective of this study is to validate the four models (Table 1) based on the angiographic and cast data of the epicardial coronary bifurcations in humans and swine, respectively. The most accurate rule based on a physical and physiological principle can then be used to determine the desired diameter of a diseased segment when the diameters of the two other segments in a bifurcation are known for percutaneous treatment of lesions.
Methods
THEORETICAL MODELS
The Murray, Finet, area-preservation (AP), and HK bifurcation diameter models are shown in Table 1. The stepwise difference between mother and large daughter vessels (i.e., Dm–Dl) is a fundamental parameter for the prediction of incomplete apposition of stent strut3, which was observed in more than 60% of non-left main bifurcation lesions2. Therefore, we determine the mother-daughter ratio Dm/Dl+Ds as a function of the daughter diameter ratio Ds/Dl (see detailed derivation in the Appendix) for the four theoretical models in Table 1, which can be angiographically used to identify the optimal stepwise difference in an epicardial coronary bifurcation. Figure 1 shows coronary bifurcations with large and small daughter diameter ratios. A comparison of the four theoretical models was carried out for the epicardial coronary bifurcations, as the daughter diameter ratio increases from zero to unity.

Figure 1. Schematic representation of bifurcations with (A) large and (B) small daughter diameter ratios.
Morphometric data and statistical analysis
The epicardial coronary bifurcations of human and swine, quantitatively determined by angiography and intravascular ultrasound3 and casts10, respectively; were used to assess the four bifurcation diameter models in Table 1. Variables were presented as mean ± standard error (SE). We also determined the relative error

between the predictions of the four models in Table 1 and the measurements. A two-way ANOVA was performed on the population of samples between theoretical models and experimental measurements, where p <0.05 represented statistically significant differences.
Results
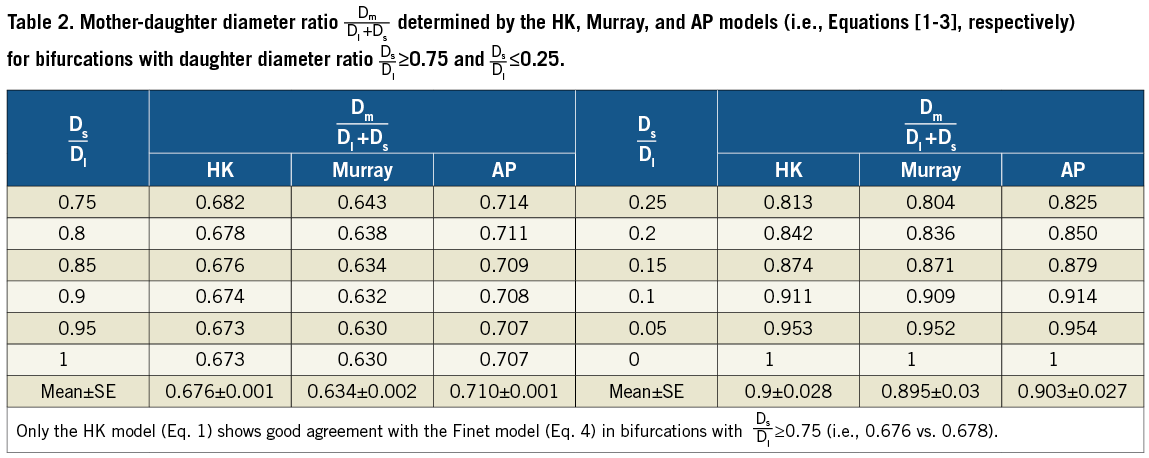
Figure 2 shows the mother-daughter diameter ratio as a function of the daughter diameter ratio obtained from the four bifurcation diameter models in Table 1 (i.e., Equations 1-4). Accordingly, Table 2 shows the mother-daughter diameter ratio determined by the HK, Murray, and AP models (i.e., Equations 1-3, respectively), which has the corresponding mean ± SE values of 0.676±0.001, 0.634±0.002, and 0.710±0.001 for bifurcations with the daughter diameter ratio ≥0.75 and 0.9±0.028, 0.895±0.03, and 0.903±0.027 for bifurcations with the daughter diameter ratio ≤0.25. This is in comparison with the Finet model that predicts a constant value of 0.678.
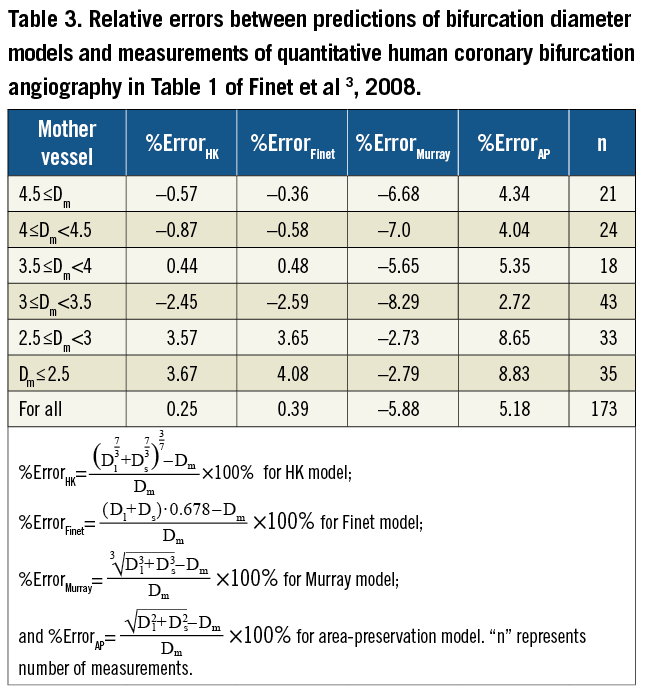
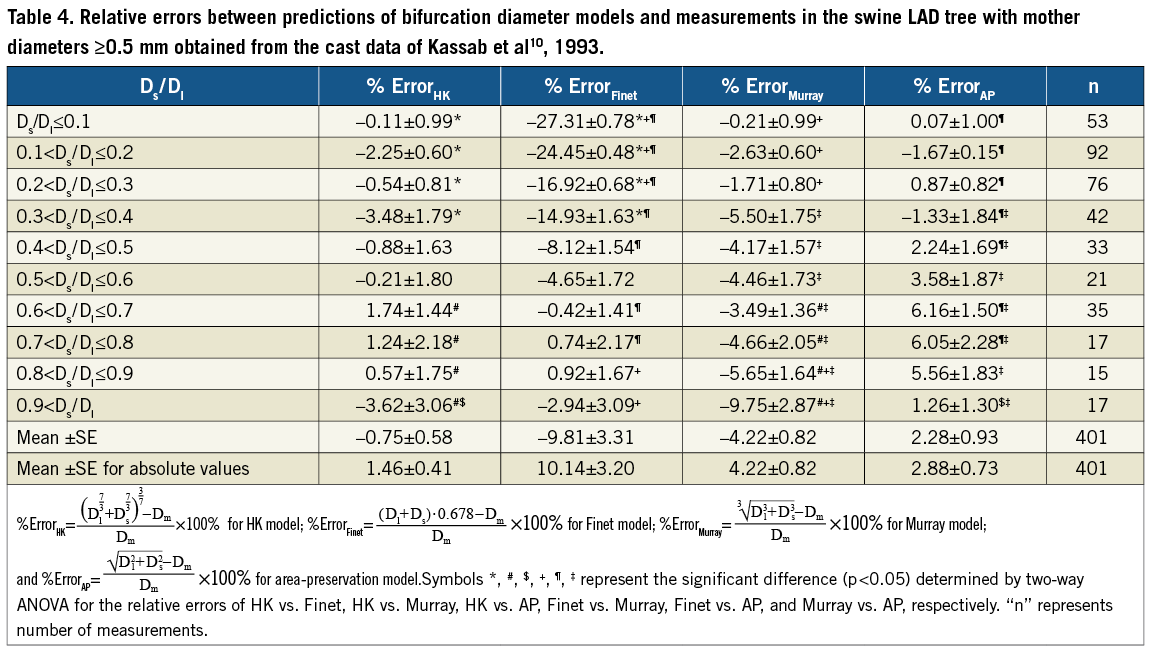
For patients, Table 3 shows the relative errors (i.e., %ErrorHK, %ErrorFinet, %ErrorMurray, and %ErrorAP) between the predictions of the four models in Table 1 and the measurements by quantitative human coronary bifurcation angiography (see Table 1 in Finet et al3). Moreover, Table 4 shows the relative errors between the predictions of the four models in Table 1 and the morphometric measurements in the swine epicardial LAD tree with mother diameters ≥0.5 mm obtained from the casts of Kassab et al10. Figure 3 also shows the relative error as a function of the daughter diameter ratio corresponding to Table 4.
Discussion
Atherosclerotic lesions tend to predominate around epicardial coronary bifurcations1,6,7. A bifurcation diameter relationship of “normal” reference is needed to restore the diameter of diseased vessel for optimal flow through the epicardial coronary bifurcation3,4. Here, we evaluated four bifurcation diameter models (summarised in Table 1) using the morphometric data from patients and swine. The major finding is that the HK and Finet models agree well with the measurements for coronary bifurcations of larger daughter diameter ratios while the HK, Murray and AP models are consistent with the experimental results for coronary bifurcations of smaller daughter diameter ratios. Hence, we conclude that the HK model is the only rule that accurately describes bifurcations of all daughter diameter ratios in the normal swine and human epicardial coronary arterial tree.
Finet et al3 have empirically shown that the mother-daughter diameter ratio Dm / Dl+Ds is 0.678 in the large epicardial coronary arterial tree, based on quantitative coronary angiography and intravascular ultrasound measurements. The Finet model agrees with the experimental measurements much better than the Murray and AP models3. Moreover, based on the minimum energy hypothesis, Huo and Kassab7 theoretically modified the Murray model as
![]()
which was validated in various vascular trees down to the pre-capillary arterioles in different organs and species. As shown in Table 3, the HK model also agreed well with the experimental measurements of Finet model. This suggests that there should be a relationship between the Finet and HK models, which is verified in the present study.
Equations 1-4 in the Appendix show the mathematical relationships between the four bifurcation diameter models in Table 1. The daughter diameter ratio Ds/Dl→1 or Ds/Dl→0 leads to different mother-daughter diameter ratios, as shown in Figure 2 and Table 2. From the HK model, the mother-daughter diameter ratio in bifurcations with Ds/Dl≥0.75 equals to 0.676, which is very similar to 0.678 of the Finet model. From the study of Finet et al3, the daughter diameter ratio was 0.828±0.024 (mean ±SD) so that the HK model is consistent with the empirical Finet model, as shown in Table 3. Figure 2 shows that the mother-daughter diameter ratio determined by Equation 1, however, deviates from the prediction of Finet model as the daughter diameter ratio decreases away from 0.75. In particular, the mother-daughter diameter ratio determined by the HK, Murray, and AP models become very similar when Ds/Dl ≤0.25. Accordingly, Table 2 shows the mother-daughter diameter ratio increases from about 0.8 to unity as the daughter diameter ratio Ds/Dl decreases monotonically from 0.25 to zero, which is significantly larger than the prediction of the Finet model. Hence, the Finet model is in gross error for coronary bifurcations with Ds/Dl <0.75, which were not considered in their study as they are less relevant clinically.
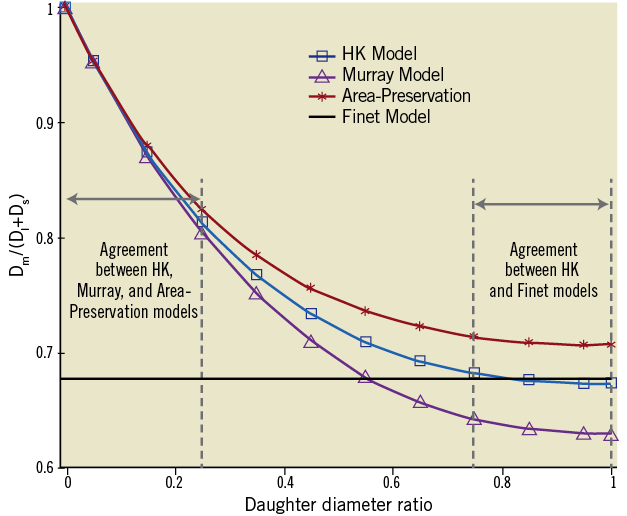
Figure 2. The relationship between the mother-daughter diameter ratio and daughter diameter ratio determined by Equations 1-4.
To accurately and critically evaluate the four models in Table 1, we used morphometric data from the casts of swine epicardial coronary arterial bifurcations10. As shown in Figure 3 and Table 4, the HK model agrees well with the measurements for all daughter diameter ratios (±4% error); the Murray and AP models agree with the measurements when Ds/Dl ≤0.25; and the Finet model agrees with the measurements when Ds/Dl ≥0.65, but not for other daughter diameter ratios. The comparison between theoretical models and morphometric measurements supports the HK model that is derived based on a physical principle.

Figure 3. The relative error as a function of the daughter diameter ratio by fitting of experimental measurements to the HK, Finet, Murray and AP bifurcation diameter models corresponding to Table 4. Only the prediction of the HK model is within ±4% error of actual value throughout the range of bifurcations.
Practical application
A practical question is how can the validated HK model be translated into clinical practice to restore diseased bifurcations to optimal dimensions? A website (http://www.et.iupui.edu/cnc/refdiacalculation.aspx) has been set up, which allows the determination of a diameter of any of the three segments of a bifurcation if two of the diameters are entered, as outlined in Figure 4. There is an entry blank for each segment. Once two of the entries are input, one can click the button “Calculate” to yield the third segment according to the HK model. This website can be downloaded to an iPhone, Blackberry, etc., providing a quick and easy rule to determine the reference diameter of a bifurcation for sizing of balloons or stents.

Figure 4. The diameter relationship determined by the HK model.
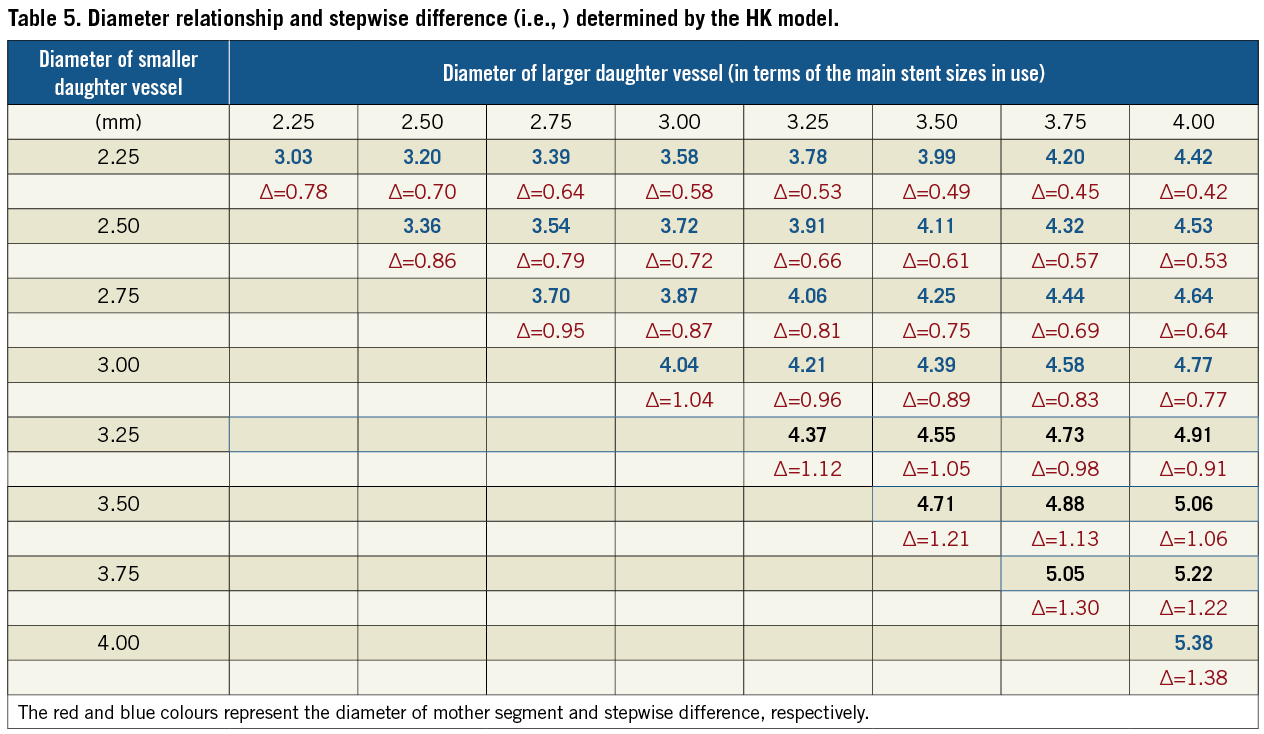
An additional approach is to provide a simple look-up chart as demonstrated in Table 5. The table contains the relationship between the mother and daughter bifurcation diameters as well as the stepwise of diameters between mother and large daughter vessels. The double-entry system in the table can be easily used to determine the diameter of mother vessel (red colour) and the stepwise difference (blue colour) based on the measured two daughter vessels.
Conclusions
This study confirmed the following conclusions:
1) The HK model accurately predicts all bifurcation types (e.g., epicardial coronary bifurcations of all daughter diameter ratios) and is based on minimum energy hypothesis;
2) The Murray and AP models are in agreement with the morphometric measurements only for bifurcations of smaller daughter diameter ratios (Ds/Dl ≤0.25);
3) The Finet model is in agreement only for bifurcations of larger daughter diameter ratios (Ds/Dl ≥0.75);
4) We have designed an easy-to-use website to determine the 3rd diameter of a bifurcation (based on the HK model) that can be downloaded to an iPhone, Blackberry, etc. as well as a look-up table.
Acknowledgement
This research is supported in part by the National Institute of Health-National Heart, Lung, and Blood Institute Grants R01-HL092048 (GS Kassab) and the AHA Scientist Development Grant 0830181N (Y Huo).
Appendix
Based on the four models in Table 1, the mother-daughter diameter ratio is expressed as a function of the daughter diameter ratio, where Dm, Dl and Ds are the diameters of mother, large and small daughters, respectively.
1) From the HK mode, the relationship between Dm/Dl+Ds and Ds/Dl is given as:
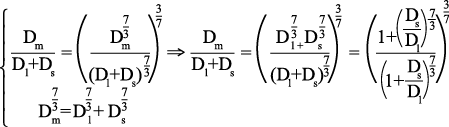 [1]
[1]
2) From the Murray mode, the relationship between Dm/Dl+Ds and Ds/Dl is given as:
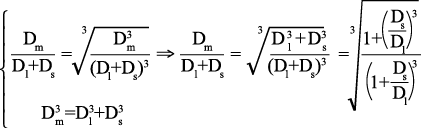 [2]
[2]
3) From the AP mode, the relationship between Dm/Dl+Ds and Ds/Dl is given as:
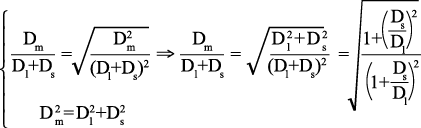 [3]
[3]
4) Finet model is given as:
Dm/Dl+Ds= 0.678 [4]
Equations 1-3 represent the ratio Dm/Dl+Ds as a function of the daughter diameter ratio Ds/Dl derived from the HK, Murray, and AP models, respectively. As the daughter diameter ratio approaches one, Equations 1-3 give 0.673, 0.63, and 0.707 for the HK, Murray, and AP models, respectively. Alternatively, as the daughter diameter ratio approaches zero, Equations 1-3 give one for the HK, Murray, and AP models, respectively.
Conflict of interest statement
The authors have no conflict of interest to declare.

