Abstract
The study of the structure-function relation of coronary bifurcations is necessary not only to understand the design of the vasculature but also to use this understanding to restore structure and hence function. The objective of this review is to provide quantitative relations between bifurcation anatomy or geometry, flow distribution in the bifurcation and degree of perfused myocardial mass in order to establish practical rules to guide optimal treatment of bifurcations including side branches (SB). We use the scaling law between flow and diameter, conservation of mass and the scaling law between myocardial mass and diameter to provide geometric relations between the segment diameters of a bifurcation, flow fraction distribution in the SB, and the percentage of myocardial mass perfused by the SB. We demonstrate that the assessment of the functional significance of an SB for intervention should not only be based on the diameter of the SB but also on the diameter of the mother vessel as well as the diameter of the proximal main artery, as these dictate the flow fraction distribution and perfused myocardial mass, respectively. The geometric and flow rules for a bifurcation are extended to a trifurcation to ensure optimal therapy scaling rules for any branching pattern.
Introduction
The structure-function relation is one of the oldest paradigms in medicine and biology. The coronary vasculature, and in particular coronary branching, provides exquisite examples of the structure-function relation1-3. The coronary branching patterns serve to distribute blood flow throughout the three-dimensional space of the heart. The study of coronary bifurcations is advisable, not only to understand nature’s design for optimal distribution of blood flow throughout the myocardium but also to use this understanding through intervention (e.g., percutaneous coronary intervention, or coronary artery bypass graft) that restores structure and hence function4.
In our last review of coronary structure-function relation in EuroIntervention4, we highlighted the various scaling laws of bifurcations based on design principles and fractal branching. This provided precise geometric relationships between the three diameters in a bifurcation where, if two of the diameters of a bifurcation are known, the third branch can be determined based on an analytical relation5,6. Here, we emphasise the relation between bifurcation anatomy or geometry, flow distribution in the bifurcation based on conservation of mass, and the percentage of perfused myocardial mass based on scaling laws. In the process, we hope to establish practical rules to guide optimal PCI for treatment of bifurcations including side branches (SB) and their functional impact. Bifurcation treatment strategy should be considered when the loss of an SB can worsen prognosis or symptoms. The EBC consensus highlighted the fact that SB diameter and length may be considered surrogates for volume of muscle at risk7.
Specifically, we will address two primary questions in this review. First, the current criteria for SB treatment tend to focus mainly on the diameter of the SB, i.e., if the SB is <2.5 mm, it is considered secondary, whereas if it is >2.5 mm, it is considered functionally significant. Clearly, functionality is associated with myocardial perfusion (flow) and hence the extent of myocardial mass perfused. Accordingly, we will relate the diameter of an SB to the fraction of blood flow in the SB and myocardial mass perfused. Secondly, although most coronary branching consists of bifurcations, coronary trifurcations are not uncommon in the left coronary artery, e.g., LAD/circumflex/intermediate artery. For these cases, it is important to extend the diameter and flow relations to guide trifurcation treatment. The discussion below lays the foundation with which to address the two questions raised.
Relation between flow and geometric rules
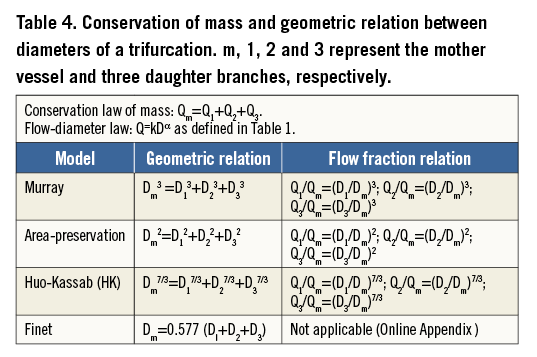
Nearly 90 years ago, Murray8 proposed a power law relation (i.e., Q~Dα) between the flow (Q) and diameter (D) of a vessel branch (Table 1). Based on the minimum energy principle and the assumption of laminar flow through a vessel, Murray’s law predicts an exponent of 3 (i.e., α=3). Fifty years later, Uylings9 argued that the exponent can vary in the range of 2.33 to 3.0 depending on whether the flow is turbulent (2.33) or laminar (3.0; i.e., Murray’s law). For epicardial coronary arteries, Kassab and colleagues3,10 have shown, both theoretically and experimentally, that the exponent equals 7/3 (2.33) despite the flow not being turbulent in these vessels. Hence, Murray and Uylings were only partially correct for the coronary bifurcations.

To relate the three diameters of a bifurcation, we use the law of conservation of mass (Table 1). If we consider a bifurcation (Figure 1), the flow through the mother vessel must equal the sum of the flow of the daughter vessels, namely, Qm=Ql+Qs (where m, l and s represent the mother vessel and the larger and smaller daughter vessels, respectively). Conservation of mass can be combined with the power law relation between flow and diameter to yield the desired relation: Dmα=Dlα+Dsα (e.g., Murray’s law is typically expressed as: Dm3=Dl3+Ds3). The diameter relations for Murray, area-preservation, Huo and Kassab (HK) and Finet are summarised in Table 1.
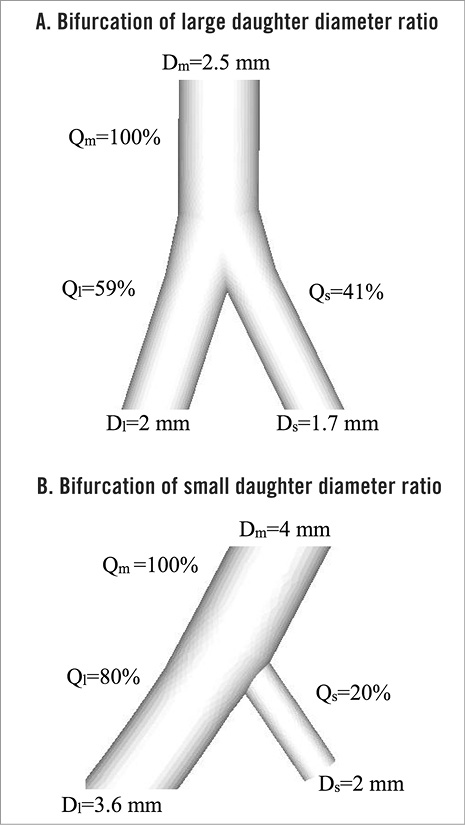
Figure 1. Examples of two different bifurcations (A and B), showing the diameter of the mother (Dm) and larger (Dl) and smaller (Ds) daughter vessels. The distribution of flow (Q) is also shown where the flow in the mother vessel is normalised at 100% and the fraction of flow in each of the branches is shown.
The Murray and HK models were based on conservation of mass and a minimum energy hypothesis for laminar flow. Murray’s exponent of 3 implies that the wall shear stress is constant throughout the vasculature, which is not supported by experimental measurements2,3. The point of departure between the HK model and Murray’s formulation is that the former considers the coronary network as an integrated whole where the downstream resistance can affect the flow through the coronary system, whereas the latter considers individual vessels in isolation. The area-preservation model simply assumes that the area of the mother vessel equals the sum of the areas of the daughter vessels, which is not supported by vascular anatomical data. This model implies that the velocity rather than wall shear stress is constant throughout the vasculature, which is also not supported by experimental observations. Finally, Finet’s model, based on a fractal geometry (Online Appendix) and validated for certain branching of human epicardial coronary arteries, has the advantage of simplicity but does not obey conservation of mass (Table 1).
To apply the formulations in Table 1 to a specific bifurcation (Figure 1), we will consider the following example. Figure 1A shows an SB of 1.7 mm that arises from a 2.5 mm mother vessel, while Figure 1B shows a 2 mm SB that branches from a 4 mm vessel. The diameters of the various segments of the bifurcation were selected to obey the HK model. In this example, we shall demonstrate that approximately similar SB diameters (1.7 vs. 2 mm) will have very different implications for the distribution of blood flow for the two bifurcations considered (Figure 1A, Figure 1B). If we normalise the flow of the mother vessel to 100%, the flow fraction in the daughter branches is determined based on the equations (under the heading of “Flow fraction relations”) in Table 1 for Figure 1A and Figure 1B. Although the SB in Figure 1A is smaller (1.7 mm), it receives a larger fraction (41%) of the mother flow than the 2 mm SB (20%), in order to satisfy conservation of flow. It is apparent that it is less acceptable to sacrifice a 2 mm SB if the daughter vessel diameters are nearly equal (Figure 1A), while a large difference in daughter vessel diameters (Figure 1B) implies that the side branch flow is relatively low. Hence, in consideration of the functionality of the SB, one should consider the mother vessel dimension and the consequent flow distribution as dictated by conservation of mass.
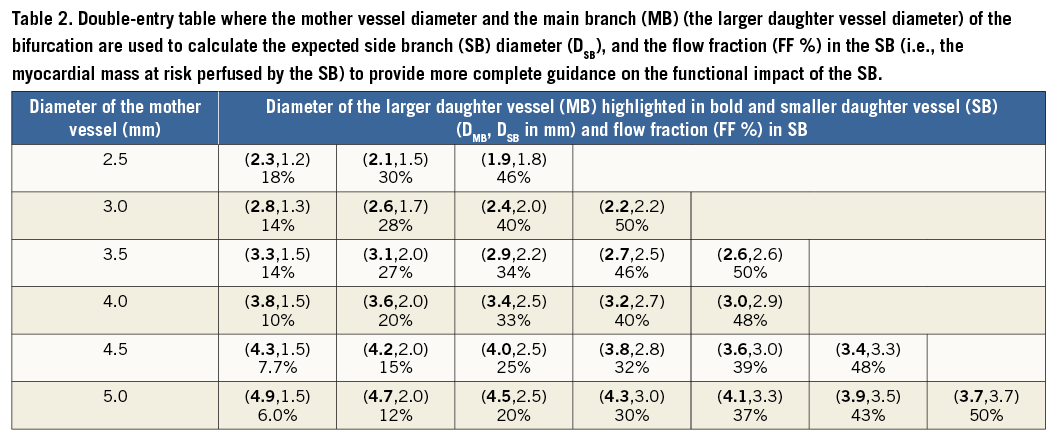
The double-entry Table 2 with both geometry and flow fractions between the daughter vessels provides guidance on bifurcation treatment strategy and the functional impact of the SB on the myocardial mass that it perfuses, which may be the at-risk myocardial mass in case of dissection or restenosis of SB.
Relation between SB and myocardial mass
In conjunction with the flow analysis described above, the major functionality of the SB hinges on the degree of myocardial perfusion provided by the SB. Accordingly, it is imperative to know the scaling relation between the diameter of a vessel and the myocardial mass perfused. Choy and Kassab11 validated a number of scaling relations between myocardial mass and morphometric parameters (e.g., lumen diameter or area of vessel, vessel length, etc.). The scaling law between myocardial mass (M) and vessel area (A) was shown to be M α A4/3 or M α D8/3, since A α D2. Kassab et al12 recently used this scaling relation between myocardial mass and SB dimension to quantify the percentage of myocardial mass perfused by the SB: (%Infarctmain artery=MSB/MMA×100=(DSB/DMA)8/3×100), where MMA and DMA represent the mass and diameter of the main artery (MA), and MSB and DSB correspond to the respective SB values. The %Infarctmain artery represents the fraction of mass perfused by the SB as compared to the entire myocardial mass perfused by the major coronary artery (e.g., LAD, LCX or RCA).
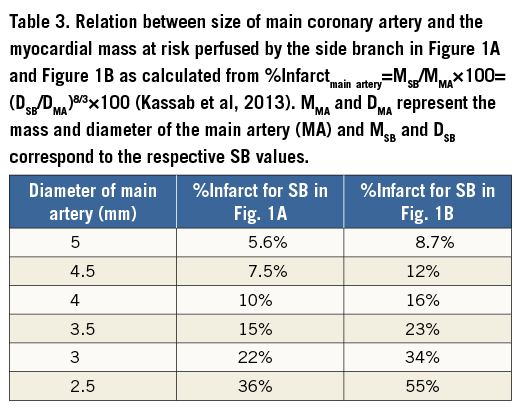
Table 3 provides an example of a calculation corresponding to the bifurcations in Figure 1A and Figure 1B. We consider the SB in each of the two examples relative to the diameter of the main branch, ranging from 5 to 2.5 mm. By definition, %Infarctmain artery is not only affected by the diameter of the SB but also by the diameter of the MB. The decision to treat the SB (e.g., if it perfuses a clinically significant myocardial mass) for the bifurcation in Figure 1A would be warranted at an MB diameter <3 mm (%Infarctmain artery=22%) and that of the bifurcation (Figure 1B) at MB diameter <3.5 mm (%Infarctmain artery=23%). Hence, in consideration of the impact of the SB on myocardial mass, one must consider both the diameter of the SB and the diameter of the proximal major coronary artery from which the distal SB arises.
Generalisation of geometric and flow rules to trifurcations
Although the formulations above apply to a bifurcation (a mother vessel giving rise to two branches), it is possible to generalise these formulations to a trifurcation (a mother vessel giving rise to three branches). This anatomic situation is rare and largely arises in the left main artery. It results in a geometry that is more complex for the interventional cardiologist for the exact sizing of the coronary artery and/or the expected stepwise difference between the diameters of the larger daughter vessel (main vessel) and of the left main. The law of conservation of mass states that the flow of a mother vessel must equal the sum of the flows in all daughter vessels regardless of the number of daughter branches (Table 4). Similarly, the flow-diameter scaling law applies to every vessel in a bifurcation or trifurcation. Table 4 summarises the geometric and flow ratio rules for a trifurcation, analogous to Table 3 for a bifurcation. The %Infarctmain artery value remains unchanged since it is defined relative to the main branch.
A website (http://ett.calmi2.org/cnc/refdiacalculation/) has been set up, which allows determination of the diameter of any of the four segments of a trifurcation if three of the diameters are entered, as outlined in Figure 2. There is an entry blank for each segment where, once three of the entries are entered, one can click on the “calculate” button to yield the fourth segment according to the HK model. In case of a bifurcation, one of the three daughter vessel segments (one, two or three) can be set equal to zero. Hence, this calculation is general to bifurcations or trifurcations. The website can be downloaded on an iPhone or iPad and provides a quick and easy rule to determine the reference diameter of a bifurcation or trifurcation for sizing balloons or stents. Figure 3 demonstrates this calculation for a patient angiogram with left main trifurcation (LAD/circumflex/intermediate artery).

Figure 2. The calculation of diameters as determined by the HK model for a trifurcation.
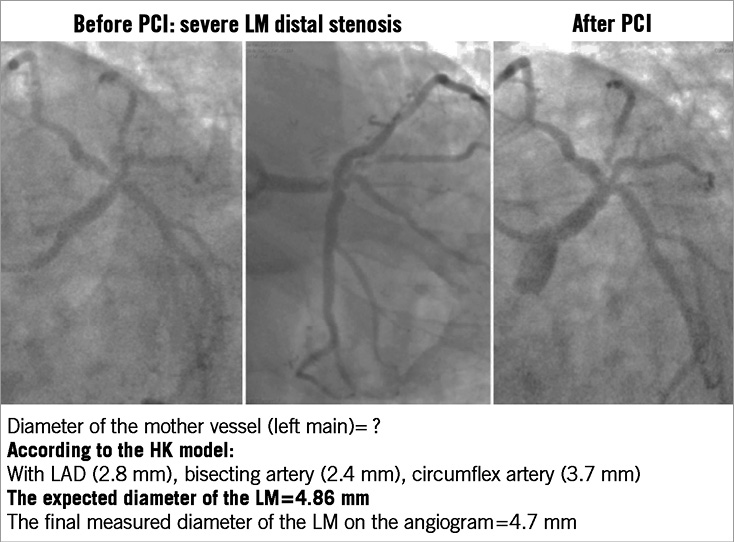
Figure 3. Example of coronary left main (LM) trifurcation (LAD/circumflex/bisecting artery). Determination of the optimal diameter at a trifurcation when the other three diameters are known, based on the relation: Dm7/3=D17/3+D27/3+D37/3.
Limitations
The above formulations assume that the myocardium is viable and the coronary vasculature obeys the scaling laws in the presence of focal disease. Recently, we have shown that the form of the scaling laws and the exponent remain unchanged in the presence of coronary artery diffuse disease in patients while the coefficient of the scaling law changes13. In the case of severe flow-limiting disease, vessel rarefaction may alter the scaling laws and the relation with the diminished infarcted myocardial mass. The latter circumstances remain to be studied and are beyond the scope of the present formulation.
Although myocardial contraction may also play a role, this effect is expected to be small, given that the majority of blood flow through the myocardium occurs in diastole.
Conclusions
SB diameter in coronary bifurcation is often a decision criterion for bifurcation treatment strategy (one or two-stent technique). In addition to diameter, visually determined angiographic SB length is considered a surrogate for myocardial mass7. Angiographic determination of SB length is limited by the resolution of the angiographic equipment, however, and the epicardial coronary arteries visualised on angiography represent only 5% of the entire coronary tree. Moreover, “true” bifurcation is usually defined by SB diameter ≥2.5 mm, and “non-true” bifurcation by diameter strictly <2.5 mm14, i.e., an absolute value that does not take into account the relative coronary flow in each of the two daughter branches. The purpose of this review is precisely to highlight the relative distribution of coronary flow in the two daughter branches. Table 2 clearly illustrates that, for a LAD/DIAG bifurcation with diameters 3.0 mm, 2.4 mm and 2.0 mm, the 2.0 mm diameter SB is small and therefore negligible. This SB, however, contributes 40% of the flow rate provided by the 3.0 mm mother vessel. Deterioration or loss of this SB may therefore have adverse effects. The problem of bifurcation classification and SB characteristics is unresolved and remains under discussion14. This review makes a definite, functional and anatomical, contribution to SB characterisation.
In conclusion, assessment of the functional significance of an SB for intervention should be based not only on the diameter of the SB but also on the diameters of the mother vessel and of the proximal main artery, as the latter dictate the flow fraction distribution and myocardial mass, respectively. The geometric and flow rules for a bifurcation are easily extended to a trifurcation to ensure optimal therapy for any branching pattern.
Conflict of interest statement
The authors have no conflicts of interest to declare.
Online Appendix
Geometry of a symmetric trifurcation of the left main coronary artery.
For an incompressible fluid, the conservation of mass is such that the sum of the outflows Qo is equal to the inflow Qi:
Qi=Qo1+Qo2+Qo3
Q=AV, where A is the arterial cross-sectional area, V is the blood-flow velocity. If the blood velocity V is the same in all four vessels, then the above equation becomes:
![]()
After simplification, we obtain:
![]()
or
![]()
If we assume a symmetric trifurcation (i.e., the three daughter vessel diameters are identical), then:
![]()
Diameters Do1, Do2 and Do3 can be reintroduced into the formula, such that:
![]()
or
![]()
The constant velocity and identical branch diameters are only a rough approximation for a simplified linear model.
The same demonstration can be made for a bifurcation (two daughter vessels), such that:
![]()
The numerical value of 0.707 is similar to 0.678 determined for the human epicardial coronary arteries (Finet et al, 2008).