Abstract
Elevation of biomarkers and ischaemia after coronary stenting of a bifurcation is not uncommon due to side branch (SB) occlusion. Hence, it is important to understand the relation between the lumen calibre of the SB and the myocardial mass affected. The objective of this proof of concept perspective is to provide a formulation for the relation between the SB calibre and perfused myocardial mass based on experimentally-validated scaling laws. A lumen calibre-mass scaling law provides a nearly linear relation between cross-sectional area of SB and the myocardial mass at risk. It is clinically known that the larger the diameter of the SB the more myocardial mass is at risk. The present analysis formulates this notion quantitatively and provides a simple relation where the %infarct can be determined directly from the angiographic cross-sectional area of SB. This relation can help guide the decision for bifurcation stenting where the SB may be at risk for occlusion. This brief proof of concept perspective provides a basis for future human studies that may demarcate the calibre (and hence myocardial mass) in relation to cardiac biomarkers as a cut-off for treatment of SB.
Introduction
It is not uncommon to find elevation of biomarkers after coronary stenting of a bifurcation as well as a potential increase in future risk of cardiac events (including post-ischaemic recovery and even mortality), sometimes due to side branch (SB) occlusion1,2. Hence, it is important to understand the relation between the lumen calibre of the SB and the myocardial mass it nourishes. The objective of this proof of concept report is to provide a theoretical foundation for the relation between the SB lumen area and perfused myocardial mass as shown schematically in Figure 1.
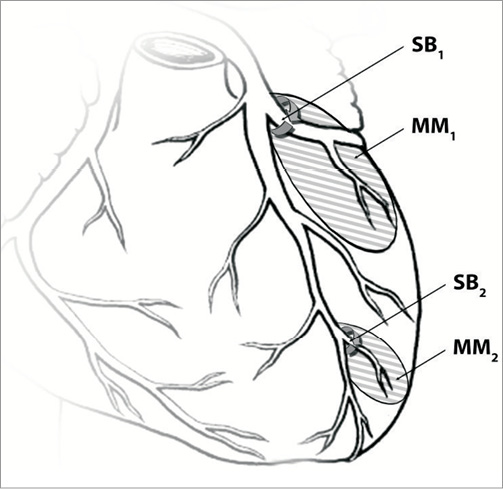
Figure 1. A schematic of the relation between side branch lumen cross-sectional area and perfused myocardial mass. MM: myocardial mass; SB: side branch
Methods
Kamiya and Takahashi3 have recently defined a relationship between the size of a coronary vessel and the volume of myocardium perfused by the vessel based on a fractal model. The infarct index was expressed as the ratio of potential ischaemic myocardium and was estimated based on the ratio of the radius of vessel of interest raised to a Murray’s exponent for the sum of similar terms for the left and right coronary arteries. Neither Murray’s exponent of 34 nor Suwa and Takahashi’s exponent of 2.75 is supported by experimental data for coronary arteries6-9. Instead, a value of 7/3 (2.33) was confirmed experimentally based on the minimum energy hypothesis6-10. Given the number of assumptions in the Kamiya and Takahashi analysis3, we provide a more basic derivation of this parameter based on actual measurements in the swine coronary vasculature.
Choy and Kassab11 related the cross-sectional area (CSA) of a vessel to the perfused myocardial mass. Based on those experimental measurements, we can define the region at risk (myocardial mass) perfused by a SB in the porcine model as follows. Let A and M represent CSA and perfused myocardial mass by the vessel of lumen area A. It was experimentally found that (A~Mα or ASB~MSBα where α=3/4)11, which is consistent with allometric scaling laws12. We define %infarct as follows:
%Infarctartery=MSB/MMA×100=(ASB/AMA)1/α×100=(ASB/AMA)4/3 ×100 [equation 1A]
where MMA and AMA represent the mass and area of the main artery (MA) and MSB and ASB correspond to the respective SB.
If we wish to determine the %infarct relative to the entire heart, we can write the following:
%Infarctheart=[MSB/(MLCCA+MRCA)]×100 = [ASB4/3/(ALCCA4/3+ARCA4/3)]×100
[equation 1B]
where LMCA and RCA stand for left common coronary artery and right coronary artery, respectively. Hence, if we know the CSA of SB of interest as well as the CSA of the main branches, we can determine the fraction of myocardial tissue at risk for infarct if the SB is occluded.
Figure 2A shows that the relation of %infarct and diameter is non-linear, whereas it is nearly linear with area (Figure 2B; e.g., %infarct=4.43ASB–4.91, R2=0.994 for LAD=5 mm). This relation allows us to determine the potential %infarct (fraction of entire artery perfused mass) from only the area of the most proximal artery (e.g., left anterior descending, left circumflex or right coronary artery; LAD, LCx, or RCA, respectively) and the lumen area of the SB angiographically.

Figure 2. Relation between A) diameter of SB and B) area of SB and %infarct (relative to the mass perfused by the most proximal artery).
Figure 2 shows four curves corresponding to LAD diameters of 3.5, 4, 4.5 and 5 mm. Obviously, the %infarct for the entire heart (equation 1B) is a smaller percent but the shapes of the curves remain the same. In either case, the relation with area is much more linear than with diameter. Hence, it is simpler to use the area of the SB relative to the main branch to estimate the potential myocardial infarct mass.
The above analysis assumes that the side branch is normal (i.e., non-diseased). Atherosclerosis can clearly affect one or more coronary vessels in the bifurcation. As such, we recently introduced a rationale for estimating the diameter of a third (stenotic) branch of a bifurcation when the diameters of the other two branches are known13. The rationale is that the optimality principle of blood flow through a bifurcation still holds as long as disease in the two “normal” branches is diffuse (<50%) rather than focal. If the SB is diseased, the diameter or area of the SB would underestimate the perfused myocardial mass. In such a case, the diameter of the SB can be determined from the mother and other daughter vessel according to the 7/3 (2.33) power law10,13 and therefore used to determine the myocardial mass at risk. Furthermore, it should be noted that the scaling laws only represent the mean behaviour of the relationship between vessel lumen calibre and myocardial mass and it cannot account for the scatter or variability in the data common to biological measurements11.
The clinical decision to treat bifurcation lesions is multifactorial14. Treatment of bifurcation lesions is complex and involves technical challenges as well as device-related factors (specialised bifurcation stents, different bifurcation stent techniques, etc.). The main point of this proof of concept study is to understand the theoretical relation between the size of the SB and the region of myocardial mass at potential risk of ischaemia or infarct. If the myocardial region at risk is significant (e.g., ~20% of the myocardial), then restoration of full blood flow through the side branch becomes the focus of the interventional therapy.
Conclusion
In summary, we provide a simple, easy to obtain index (from angiography) that provides the myocardial region at risk perfused by the SB. This relation can help guide the decision for bifurcation stenting where the SB may be at risk for occlusion. The present analysis formulates the intuitive notion that the larger the diameter of the SB, the more myocardial mass is at risk quantitatively. It provides a simple relation where the %infarct can be determined directly from the angiographic calibre of SB. This provides a basis for future human studies that may demarcate the calibre (and hence myocardial mass) in relation to cardiac biomarkers as a cut-off for treatment of SB.
Acknowledgements
This research was supported in part by the NIH National Heart, Lung, and Blood Institute Grant HL092048-5.
Conflict of interest statement
The authors have no conflicts of interest to declare.

