Abstract
Aims: To investigate the impact of balloon inflation pressure and balloon diameter on the expansion forces exerted in a stenosed vessel (congenital heart disease applications) using computational models.
Methods and results: A simplified three-dimensional model of a vessel with a cylindrical stenosis was created. Two low-compliance balloons with different inflation diameters (10 vs. 16 mm) were modelled. Finite element simulations of balloon expansions were performed. To dilate the stenosis from 4 to 10 mm lumen diameter, the large balloon needed less inflation pressure than the small balloon (0.55 vs. 1.00 MPa). Under these circumstances, the large balloon also achieved higher stresses at the stenotic vessel site (5.23±0.10 vs. 3.97±0.04 MPa, p<0.001). When using inflation pressures that led to equal surface stresses of both balloons, the large balloon could exert higher expansion forces onto the stenotic site, achieving higher stresses (5.18±0.09 vs. 3.38±0.01 MPa, p<0.001) and greater lumen diameter (9.73 vs. 8.68 mm).
Conclusions: In a computerised model of balloon dilatation, balloon diameter had a greater impact on the expansion force than inflation pressure. This finding emphasises the importance of choosing an appropriate balloon diameter to achieve optimal haemodynamic outcomes.
Introduction
In paediatric cardiology, balloon interventions are frequently used to relieve stenosis of valves, vessels or surgically placed conduits. However, the search for the “optimal balloon” to achieve maximum stenosis reduction with minimum risk remains a significant challenge in clinical practice. Although early studies in interventional cardiology demonstrated the relevance of balloon diameter for dilatation results1,2, inflation pressure is often believed to represent a more powerful determinant of angioplasty results than balloon diameter. In order to improve balloon angioplasty results, different strategies have been applied mainly driven by the idea that high inflation pressures result in high dilatation forces and, therefore, successful stenosis release. However, only small balloons3 can tolerate high inflation pressures with low risk of rupture. This limits the potential applications to small vessels and small expansion diameters.
In order to understand fundamental balloon mechanics better, we sought to analyse separately the impact of inflation pressure and diameter on the final lumen diameter and wall stress generated at an idealised stenotic site. We used finite element (FE) analysis to virtually simulate balloon inflation in a simplified model of a stenotic artery, to study and compare stress magnitudes and distribution caused by balloons with different diameters4.
Methods
Finite element model
A three-dimensional model of a simplified artery was created as a vessel with length=32 mm, lumen diameter=18 mm, wall thickness=1 mm, and a discrete, concentric, cylindrical stenosis of following dimensions: length=4 mm; stenosis thickness=7 mm; remaining lumen diameter=4 mm (Figure 1A). This obstruction corresponds to a 78% reduction in luminal cross-sectional area. The arterial tissues were modelled as isotropic and homogeneous, with hyperelastic behaviour as reported by Holzapfel et al5 for a circumferential stress response. A hyperelastic, isotropic constitutive model based on a reduced polynomial strain energy density function was adopted to describe the stenosis properties (C10=0.61, C20=37.12, C01=0.63, C11=–87.55, C02=52.30).

Figure 1. Four phases of the 10 mm balloon inflation process in the stenotic artery and correspondent changes in the balloon surface stresses.
Two different nominal balloon diameters were investigated: 10 mm (balloon-to-lumen ratio=2.5, “small”) and 16 mm (balloon-to-lumen ratio=4, “large”). The balloons were <18 mm in diameter to avoid contact between the terminal parts of the balloons and the arterial wall, thus avoiding confounding results and simulation artefacts. For both balloons, the wall thickness was 0.06 mm and the ratio between balloon diameter and length was 0.42. The balloons were assumed to have low-compliance and to be made of Nylon with linear elastic behaviour (Young modulus=2,105 MPa, Poisson ratio=0.3, ultimate tensile strength=130 MPa and density=1,100 kg/m3).
Finite element (FE) analysis
The FE commercial code ABAQUS/Explicit 6.5 (Simulia, Inc., Providence, RI, USA) was used for this study. FE analysis was performed to simulate the balloon angioplasty procedure. Dilatation was achieved with a constant balloon inflation rate for both balloons (3 atm per second) up to an internal pressure of 15 atm. A frictionless contact algorithm was defined to describe the interaction between the balloon and the stenosis. Variables analysed during this simulation were: inflation pressure needed for dilatation; wall stress (Von Mises stress, σ, a scalar function that represents the overall stress magnitude) generated during change of luminal diameter from 4 mm to a maximum of 10 mm; and change in lumen diameter at the site of stenosis.
In addition, to compare lumen dilatation below balloon burst pressure, we analysed the results at the same balloon stress distribution (maximum σ=58 MPa), which served as a hypothetical determinant of polymeric material failure stress and therefore as an indicator for risk of balloon rupture.
Statistics
Data are expressed as median±standard error of the mean. Colour coding for stresses ranged from blue (indicating low stress) to red (indicating high stress). Where applicable, the Mann-Whitney U-test was used. Statistical significance was inferred for p values <0.05. Statistical analysis was performed on GraphPad Prism 2.01 (GraphPad Software, San Diego, CA, USA).
Results
Balloon behaviour during inflation
During pressure application, the balloon ends expanded first followed by the central portion (Figures 1B-D). These changes of balloon morphology were accompanied by increases in balloon surface stresses up to 80 MPa. Initially, these stresses were localised at the site of contact between the balloon and the stenosis (Figure 1B), but then gradually distributed over the whole balloon (Figure 1C) to finally form a uniform pattern when the balloon was fully deployed (Figure 1D).
Dilatation results
In order to dilate the stenosis from 4 to 10 mm lumen diameter, the large balloon required less inflation pressure than the small balloon (5 vs. 10 atm, Figure 2A). Furthermore, at the same lumen diameter (10 mm) and despite using less inflation pressure, the large balloon caused higher stresses at the stenotic site compared to the small balloon (5.23±0.10 vs. 3.97±0.04 MPa, p<0.001, Figure 2B). After the nominal balloon diameter was reached for each balloon (10 and 16 mm), further increases in inflation pressure did not significantly change the stress distribution in the arterial wall (Figure 3).
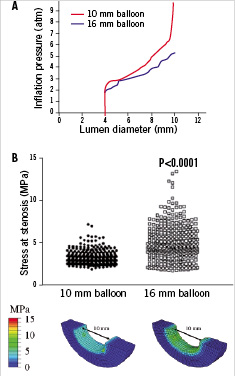
Figure 2. A: Required inflation pressure to dilate the stenosis from 4 to 10 mm lumen diameter using the small and large balloon (10 vs. 5 atm). B: At 10 mm of lesion dilatation and half inflation pressure, the large balloon caused higher stresses at the stenotic site compared to the small balloon (5.23±0.10 vs. 3.97±0.04 MPa, p<0.001).
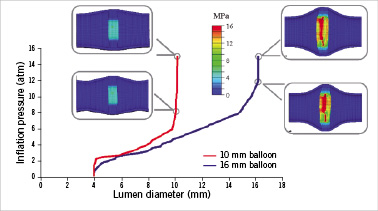
Figure 3. After the balloon nominal diameter was reached further increase in inflation pressure did not significantly change the stress distribution in the arterial wall for both balloons.
Dilatation results at equal risk of balloon rupture
At equal surface stresses on the polymeric balloon (Figure 4A), the large balloon achieved a greater lumen diameter than the small balloon (9.73 vs. 8.68 mm, Figure 4C), and higher stresses at the stenotic site (5.18±0.09 vs. 3.38±0.01 MPa, p<0.001, Figures 4B-C).

Figure 4. Below burst pressure (same stress level on the balloons before material rupture, A), the large balloon achieved higher stresses at the stenotic site (5.18±0.09 vs. 3.38±0.01 MPa, p<0.001, B-C) and a greater lumen diameter compared to the small balloon (9.73 vs. 8.68 mm, C).
Discussion
Although balloon dilatation is a common intervention for native or recurrent stenosis of vessels, valves and surgically placed conduits in congenital heart disease, there are lesions that are difficult to dilate and require careful compromise between inflation pressure and balloon diameter. The use of high-pressure balloons is thought to result in higher chances of success. The contribution of the balloon inflation pressure to the expansion forces is unequivocal; however, high-pressure balloons have smaller diameters and, sometimes, the use of a large balloon even at low pressure can result in more efficient dilatation. Size and pressure do not equally contribute to the dilatation force: there is a non-linear relationship between these parameters, which makes the problem difficult to interpret using simple physics principles. We have therefore developed a computational model of balloon dilatation to study the concurrent effects on the lesion of these two parameters – balloon pressure and diameter. This analysis has shown that the balloon diameter has a higher impact on the expansion forces than the inflation pressure.
There are two radial effects that contribute to the expansion of the stenotic artery: a direct component due to the direct application of pressure by the balloon to the stenosis surface, and an indirect force component dependent on balloon geometry and inflation stage. To understand the impact of this indirect component on the resulting expansion force, the balloon-stenotic artery system could be simplified with an uplift model, where the balloon profile is compared to a wire with a given weight (=stenosis) (Figure 5). The wire is pulled at its ends by the force F, which represents the force in the longitudinal direction due to the uniform pressure applied inside the balloon. The force F induces an indirect radial force component Fr=2Fcosφ, which pushes the weight upwards (Figures 5A-B). Once the wire is completely stretched, equivalent to full expansion of the balloon, the indirect radial force component reduces to zero (Figure 5C), and further increase in inflation pressure in the fully expanded balloon cannot add indirect force. In our simulation when the lesion is dilated to 10 mm using the large balloon, the indirect radial force component, although with a smaller angle φ*, remained effective. This did not happen in the small balloon which was already fully inflated (Figures 5B-D).
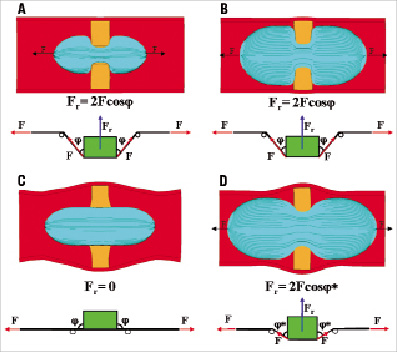
Figure 5. Impact of balloon size on radial force Fr simplified with an uplift model, where the balloon profile is compared to a wire with a weight (=stenosis). A: 10 mm balloon. B: 16 mm balloon. C: 10 mm balloon fully expanded (vessel lumen=10 mm). D: 16 mm balloon expanded up to 10 mm vessel lumen.
Technically, balloon material and resistance to rupture at a given wall stress, also determine the force of dilatation. To account for mechanical properties of the balloon, we re-calculated the impact of balloon inflation pressure and diameter on expansion forces under the assumption of equal material failure stress profiles, equivalent to the risk of balloon rupture. Importantly, this investigation reconfirmed the superior dilatation results of the large balloon.
On the product label for angioplasty balloons only limited information about their performance is provided to users. Information about the pressure needed to reach the nominal diameter and balloon burst pressure is useful to avoid complications. However, this may not contribute to our knowledge of predicting a successful result.
Furthermore, a better understanding of the contribution of wall stress, at a given inflation pressures may help the interventional cardiologist to anticipate the performance of the balloon used. We have shown that further increase in inflation pressure in a fully expanded balloon did not increase lumen diameter or vessel wall stress. This is of particular interest for clinicians and industry6, since balloon rupture influences success and safety of balloon intervention. At the other end of safety considerations, a high balloon-to-lumen diameter ratio carries the risk of vessel damage (dissection or rupture)7, most likely at the non-stenosed part of the vessel adjacent to the stenotic site. Therefore, careful choice of balloon size has to be considered individually before embarking on interventional procedures8-9.
Limitations
Our work is based on a simplified model of a complex anatomical situation. For methodological reasons the balloon sizes chosen were less than the maximum vessel diameter, which does not necessarily reflect clinical practice, but allowed us to explain the specific effects of each parameter (balloon size and pressure) on the final result (dilatation of the lesion) without confounding effects.
Conclusion
In a computational model of balloon dilatation, the balloon diameter had a higher impact on the expansion forces than the inflation pressure, highlighting the importance of choice of appropriate balloon diameter.

