Abstract
Aims: Coronary artery bifurcations present a harmonious asymmetric geometry that is fractal in nature. Interventional treatment of bifurcation lesions is a major technical issue. The present study is aimed at a precise quantification of this geometry in the hope of deriving a formulation that would be simple to calculate.
Methods and results: Forty seven patients with strictly normal coronarographic results obtained ahead of valve replacement were enrolled, and 27 of these underwent IVUS examination to confirm that their arteries were indeed normal. Three reference diameters were measured: those of the mother vessel (Dm) and of either daughter vessel (Dd1, Dd2).
One hundred and seventy-three bifurcations were thus subjected to quantitative analysis. The mean diameter of the mother vessels was 3.33±0.94 mm, of the major daughter vessels 2.70±0.77 mm, and of the minor daughter vessels 2.23±0.68 mm. The ratio R=Dm/(Dd1+Dd2) of mother-vessel diameter to the sum of the two daughter-vessel diameters was 3.39/(2.708+2.236)=0.678. This ratio held at all levels of bifurcation: i.e., whatever diameter the mother vessel.
Conclusion: The study confirmed the fractal nature of the geometry of the epicardial coronary artery tree, and gave a simple and accurate fractal ratio between the diameters of the mother and two daughter vessels such that Dm=0.678 (Dd1+Dd2). This makes it easy to calculate the precise diameter of any of the three vessels when those of the other two are known.
Introduction
Their haemodynamic particularities make arterial bifurcations liable to focal and eccentric atherosclerosis1,2. Interventional treatment of atherosclerotic coronary bifurcation lesions is a major technical issue3. Being able to determine one bifurcation vessel’s diameter on the basis of those of the other two, to detect diffuse atherosclerotic infiltration in one vessel in a bifurcation, such as left coronary trunk infiltration, to measure the best diameters in a stenotic coronary bifurcation, or to decide on the optimal design for innovative bifurcation-dedicated stents, are among the current issues facing interventional cardiologists in daily practice.
Arterial bifurcations are the morphological entities underlying the distribution of blood-flow within organs via a stepwise adaptation of vascular calibre down to the capillary level where exchange takes place. Coronary arterial bifurcations are a case in point. The adaptation consists in harmonious asymmetric geometrical reduction according to the law of conservation of energy4. The coronary tree has been shown to display morphological self-similarity – or, in other words, to be governed by fractal geometry5. A fractal object consists of a pattern, often quite simple and easy to describe, that is similar at whatever level of observation: this is known as self-similarity or homothetic invariance6. There have been numerous attempts to model arterial bifurcations7,8, but no simple formula of practical use to interventional cardiologists is currently available.
The aims of the present study were threefold: 1) to quantify normal coronary artery bifurcations – the diameters of the mother and two daughter vessels – from a detailed angiogram (this was done using a new quantitative coronary angiography software package specifically dedicated to quantifying coronary bifurcations), normal arterial status having been confirmed by intravascular ultrasound (IVUS) examination of a sub-group of patients; 2) to confirm the self-similarity – i.e., the fractal nature – of the bifurcations within an epicardial coronary tree; and 3) to derive a fractal formula for the bifurcation geometry that would be of use to interventional cardiologists, and to compare this to the existing validated physical models.
Methods
Study population
Eighty-seven patients under the age of 55 years, free of cardiovascular risk factors (diabetes, smoking, high blood pressure, or dyslipidaemia), and with strictly normal coronary angiographic results obtained ahead of valve replacement surgery, were enrolled. Only 59 of them were finally included, as meeting the methodological requirements for angiographic analysis. All patients signed an informed written consent form, and the study was approved by the institution’s Ethics Committee.
Angiographic analysis
Normal coronary angiography was defined by a strictly parallel lumen edge without detectable arterial abnormality anywhere on the epicardial angiogram. Angiography used the AdvantX® L/C Angiography System (GE Healthcare, Chalfont St. Giles, United Kingdom). The projection image was sensitive to all geometric distortions inherent in variations in the angle of incidence. In the summation image, overlapping planes meant that the vascular segment of interest was often masked by vascular branches of the coronary tree. To minimise any geometric distortion, an angiographic system featuring three motor-driven rotation axes used in tandem with a software program dedicated to determining the direction of an arterial segment-of-interest is currently available (INNOVA®, GE Healthcare). This configuration offers the operator the possibility of obtaining optimised coronary angiographic views by vessel profiling. The system ensures that the arterial segment-of-interest is strictly perpendicular to the X-ray beam. The coronary angiograms were required to be rigorously normal, with strictly parallel lumen edges9,10.
A newly developed angiographic quantification software package automatically detects and quantifies coronary bifurcations. A proximal point is placed on the mother vessel and a distal point on the first daughter vessel, then another point on the mother vessel and distal point on the second daughter vessel. The detection algorithm determined the vessel contours and traced the two vascular axes creating the bifurcation by interpolation. Three reference diameters were measured: those of the mother vessel and of either daughter vessel. Each reference diameter was located in an artery segment adjacent to the bifurcation (mother vessel and two daughter vessels) with no other neighbouring bifurcation (see Figure 1).
Figure 1. Arterial bifurcations in the coronary tree. A) Succession of morphologically self-similar coronary tree bifurcations at whatever scale of observation. B) One bifurcation selected for analysis (white circle): the arterial segments of the bifurcation (one mother and two daughter vessels) remain geometrically unchanged if no other bifurcation appears (white arrows). B’) Tracing the arterial contours by interpolation, the reference diameters lie on each compatible adjacent segment.
The bifurcation angles were also calculated.
IVUS analysis
A sub-group comprising the first 27 consecutive patients of the 59 finally enrolled underwent IVUS examination of the left trunk bifurcation, left anterior descending and circumflex arteries. Qualitative analysis confirmed the normal coronary arterial status expected in the light of the angiographic aspect. The normal three-layer appearance was required to be detected on IVUS with no intimal thickening in excess of 300 microns. This qualitative analysis recorded the mother vessel (left trunk) lumen area and those of the two daughter vessels (LAD and circumflex arteries) over the first 5 mm after the bifurcation.
The normality of arteries appearing normal on angiography was confirmed by IVUS in these patients, the results justifying normal status claimed on the basis of angiography alone. The mean relative differences in angiographic and IVUS diameters were –4.38%±5.09, –4.31%±5.3, and –5.51%±5.92% for the left trunk, LAD artery and circumflex artery, respectively. IVUS values were thus slightly greater than those given by angiography.
Theoretical formulations
LINEAR GEOMETRY
For each bifurcation, the ratio between the sum of the daughter-vessel diameters and the mother-vessel diameter was calculated. These ratios were then related to each mother-vessel diameter, so as to apprehend any self-similarity across levels of observation.
I.e., the ratio = Dm/ (Dd1 + Dd2), where Dm is the diameter of the mother vessel, and Dd1 and Dd2 are the respective diameters of the two daughter vessels.
MURRAY’S LAW
Murray was the first to describe the mother/daughter-vessel relations in vascular bifurcations, in terms of a cost function: i.e., the sum of function power loss and metabolic power dissipation proportional to blood flow. Murray described the optimal conditions for vascular bifurcation, known as Murray’s law, which states that the cube of the radius of the mother vessel equals the sum of the cubes of the radii of the daughter vessels: Dm3=Dd13+Dd23. 7
LAW OF FLOW CONSERVATION
The law of flow conservation derives from that of the conservation of energy. The sum of the daughter-vessel flows in a bifurcation equals the inflow to the mother vessel, whence Dm2=Dd12+Dd22. 4
Determining the inaccuracy on angiography of the application of the law
We sought to estimate the degree of inexactitude, with reference to the angiographic value, of applying the law of linear geometry to calculate the diameter of a vessel.
INEXACTITUDE OF A PARAMETRIC FUNCTION
Let g be a function of n parameters xi : i.e., g(x1, x2;..., xn)
σxi: Absolute inexactitude of parameter xi.
σg: Absolute inexactitude of function g.
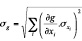: theoretical inexactitude formula for a multi-parametric function, where ∂g/∂xi is the partial derivative of g in relation to xi.
THEORETICAL INEXACTITUDE OF THE LAW
When our law is used to estimate Dm from the estimated daughter-vessel diameters, the resultant error in the estimation of Dm is to be quantified. The daughter-vessel diameters are estimated
by measuring them in pixels in the image and calculating the associated calibration factor.
Bearing in mind that D= f.Dpix, where Dpix is the measured vessel diameter in pixels in the image and f is the calibration factor associated to the image, g and its inexactitude can be defined as:
g(x1, x2,..., xn)=g(R, f, Dd1, Dd2)=R.f.(Dd1+Dd2)=f.Dm
where:
Dpixd1 is the diameter of daughter-vessel 1 (in pixels); Dpixd2, the diameter of daughter-vessel 2 (in pixels); Dpixm, the diameter of the mother-vessel (in pixels); f, the calibration factor (in mm/pixels) associated to the image; f.Dpixm =Dm, the estimate of the target mother-vessel diameter (in mm); R, the ratio of the law; σf, the absolute inexactitude of the ratio; Δ%R, the percentage inexactitude of the ratio; σDpix, the absolute inexactitude on the measurements; σf, the absolute inexactitude (in mm/pix) on the calibration factor; Δ%Dpix, the percentage inexactitude on the measurement of Dpix in the image; and Δ%f, the percentage inexactitude on the measurement of f.
With Δ%D=σD.100D and Δ%f=σf.100f
LITERATURE DATA
Δ%D= 1% on phantom11
Δ%D= 5% on 6 Fr catheter or on frontal autocalibration12,13
Statistical analysis
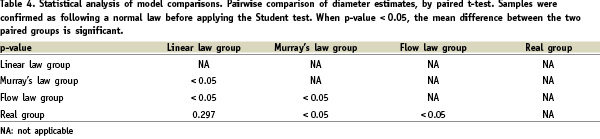
Variables are presented as mean ± SD. Diameters and diameter variations were compared by paired t-test. It was checked that the samples followed the Normal law before applying the Student test. Probability values of <0.05 were considered statistically significant. All computations were performed with StatView® 4.0 (Abacus Concept Inc.).
Results
Quantitative coronary bifurcation angiography data base
The coronary artery tree comprises a succession of vascular bifurcations (see Figure 1). Fifty-nine patients, 35 female and 24 male, of mean age 46±8.5 years, were included. One hundred and seventy-three bifurcations – i.e., 2.9 bifurcations per patient – were subjected to angiographic analysis. Mean mother-vessel diameter was 3.33±0.94 mm, mean major daughter-vessel diameter 2.70±0.77 mm and mean minor daughter-vessel diameter 2.23±0.68 mm. The mean stepwise difference between mother- and major daughter-vessel diameters was 0.631±1.05 mm: i.e., a 19% reduction on the mother-vessel diameter. The angles between the mother- and major daughter-vessel and between the two daughter vessels were respectively 156°±29° and 60±28°.
Self-similarity and fractal ratio
The ratio R=Dm/(Dd1+Dd2) between the mother-vessel diameter and the sum of the daughter-vessel diameters was 3.39/(2.708+2.236)= 0.678 for the 173 bifurcations. In the group of 27 patients examined by IVUS, R(angio)=0.0670±0.031 and R(IVUS)= 0.668±0.028 (p=NS).
This ratio was constant whatever the scale of observation – i.e., whatever the mother-vessel diameter (Table 1).
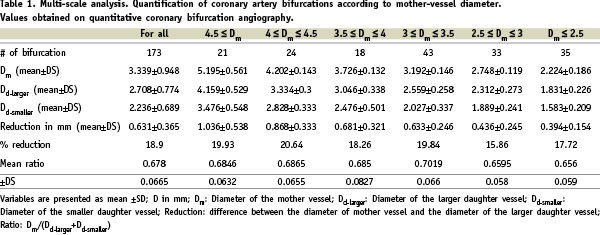
The coronary tree thus presents a fractal geometry, with the above ratio as the fractal dimension. The relative reduction between the mother- and major daughter-vessel diameters was likewise constant at all scales of observation, at around 19%, but with an absolute value that increased with the mother-vessel diameter.
DETERMINING THE INACCURACY ON ANGIOGRAPHY OF THE APPLICATION OF THE LAW
Application in 3 examples of representative bifurcations:
Left trunk bifurcation
f.Dd1= 3.5 mm (LAD artery), f.Dd1=3 mm (Circumflex artery), f=0.14 mm/pixel and R=0.678
Estimate of left trunk: f.Dm=0.678.(3.5+3)=4.407 mm
Applying (F) with σR=0 gives a relative inaccuracy of 5.05%: i.e., a quantitative angiography uncertainty of 0.22 mm in the estimate of 4.407 mm for the mother-vessel diameter.
LAD bifurcation
f.Dd1= 3 mm, f.Dd1= 2.5 mm, f = 0.14 mm/pixel,and R=0.678
Estimated mother-vessel diameter: f.Dm= 0.678.(3+2.5)=3.729 mm
Applying (F) with σR=0 gives a relative inaccuracy of 5.05%: i.e., a quantitative angiography uncertainty of 0.19 mm in the estimate of 3.729 mm for the mother-vessel diameter.
Small vascular bifurcation
f.Dd1= 2 mm,f.Dd1= 1.5 mm,f = 0.14 mm/pixel, and R=0.678
Estimated mother-vessel diameter: f.Dm= 0.678.(2+1.5)=3.051 mm
Applying (F) with σR=0 gives a relative inaccuracy of 5.05%: i.e., a quantitative angiography uncertainty of 0.15 mm in the estimate of 3.051 mm for the mother-vessel diameter.
Comparison with theoretic models
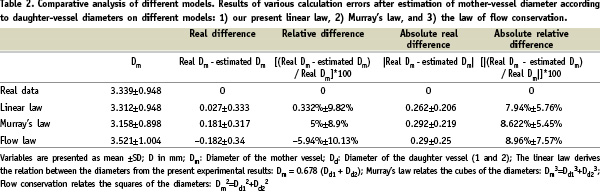
The above linear law enables mother-vessel diameter to be estimated from the two daughter-vessel diameters to within 0.33%, without bias. Table 2 presents the comparative analysis.
Multi-scale analysis further showed the estimate derived from the linear law to be precise whatever the mother-vessel diameter (Table 3).
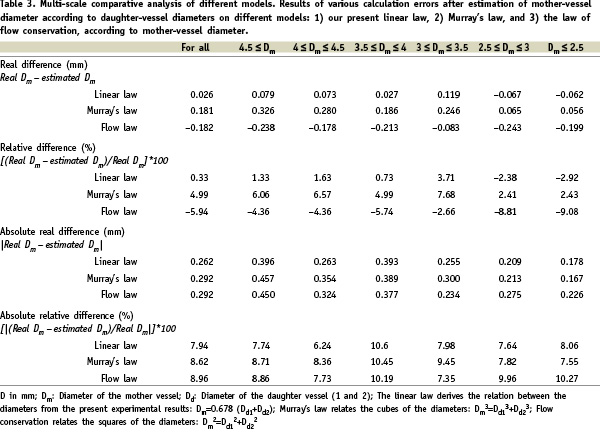
Murray’s law tends to overestimate and the law of flow conservation to underestimate mother-vessel diameter (see Figure 2), with deviations of respectively 0.33%, 5% and 5.94% for the linear law, Murray’s law and the conservation law.
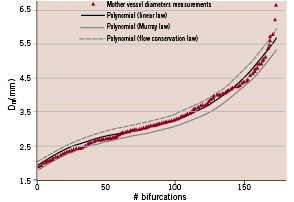
Figure 2. Distribution of the 173 sets of mother-vessel diameters, as measured and calculated according to the 3 laws. The linear law (R=0.678) is found to be the most exact: the flow conservation law overestimates and Murray’s law underestimates the calculated mother-vessel diameter.
Finally, Table 4 shows that the linear law alone estimates mother-vessel diameter from the daughter-vessel diameters without statistically significant deviation from real values.
Discussion
The present study confirms the fractal nature of epicardial coronary arterial tree geometry and provides a simple fractal ratio relating mother-vessel diameter (Dm) and the daughter-vessel diameters by the formula: Dm=0.678 (Dd1+Dd2). Consequently, one daughter-vessel diameter can easily be calculated when the other daughter-vessel diameter and the mother-vessel diameter are known: Dd(1 or 2)=(Dm/0.678) – Dd(2 or 1). These calculations prove exact – more so than those derived from Murray’s law or the law of conservation of flow, which moreover are much more complex in their formulations.
Biological tree structure
Many authors have studied and formalised the relations underlying the branching pattern and vascular geometry of the biological tree structure5,7. The relations seem to be complex, governed by a set of scaling laws which are based on the hypothesis that the cost of construction of the tree structure and operation of fluid conduction are minimised. The laws consist of scaling relationships between 1) tree length and vascular volume, 2) lumen diameter and blood flow rate in each branch, and 3) vessel branch diameter and length. The expression of these formulations is complicated by the insistence on generalising a law to the whole set of biological branching patterns14,15.
Coronary bifurcation and fractal geometry
It is now well-established that the coronary arterial tree displays self-similarity patterns6. There is, however, no formulation of this available that would be practical for the purposes of an interventional cardiologist. To the best of our knowledge, only one study, on just 20 left coronary trunk angiograms, has quantified the ratio between the sum of the daughter-vessel diameters and the mother-vessel diameter; the ratio here came out at 0.65±0.04 – very close to our present result16.
The interesting study by Costa et al of coronary bifurcation lesions treated with the “crush” technique indirectly confirms that fractal geometry – and thus optimal flow physiology – is restored after stenting17. Their IVUS data for treatment of the left trunk confirm this with a mean proximal reference lumen cross-sectional area of 16.5 mm2, a distal reference lumen cross-sectional area of 8.6 mm2, and a mean side-branch distal reference lumen cross-sectional area of 8.5 mm3, corresponding to diameter values of 4.55 mm, 3.32 mm, and 3.30 mm respectively. Their Dm/Dd1+Dd2 ratio came out at 0.687 – very close to the fractal ratio of 0.678, thereby confirming the geometric and hence functional quality of the left-trunk percutaneous coronary interventions.
Impact for interventional cardiology
Determining vascular reference diameters in bifurcations
Knowing two out of three angiographically normal or near-normal diameters in a bifurcation enables straightforward calculation of the third. Even if the vessels are not exactly normal angiographically, the calculation will at worst suffer from underestimation, and will certainly not give an excessive value that might hazardous for intervention. Percutaneous coronary intervention seeks to restore a functionally normal lumen: i.e., one obeying these laws of hydraulics, or more precisely of haemodynamics.
Angioplasty seeks to restore normal flow in each axis of a bifurcation, whatever the condition of the normal or atherosclerotic wall due to positive or negative remodelling. This is a vascular conduction network, and only the arterial lumen diameters affect flow and coronary haemodynamics. The fractal ratio gives the distribution of the endoluminal diameters of each branch, which determine the section areas, which in turn determine the blood flow rate (the function in this case creating the organ). Angioplasty therefore seeks to restore optimal endoluminal diameters so as to optimise flow distribution: i.e., so that the sum of daughter-vessel blood flow rates (outflow) should equal the mother-vessel flow rate (inflow); such is the law of conservation of energy.
Thus, diffuse atherosclerotic left coronary trunk infiltration can easily be detected on the angiogram, as the example shown in Figure 3 bears witness.
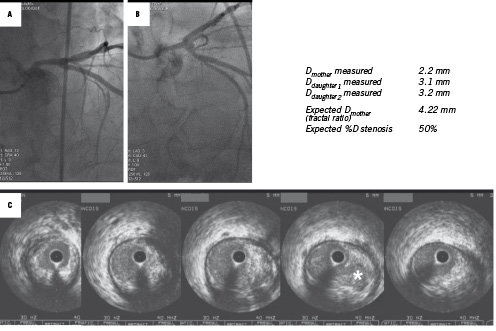
Figure 3. Example of stent apposition defect in the main vessel (LAD artery) undetected on angiography (A). The 3.0 mm stent diameter as determined on IVUS (B) was optimal for the daughter vessel (downstream LAD artery), but too narrow for the 3.85 mm mother vessel, with a stepwise difference of 0.85 mm easily detected on IVUS cross section (C). Final kissing balloon inflation corrected this defect by locally increasing the overall inflation diameter.
Many intravascular ultrasound (IVUS) studies have spotlighted failure to detect atherosclerosis on simple coronary angiography18,19. IVUS examinations, however, are routine in only a very few catheterisation laboratories.
Precise quantitative coronary bifurcation angiography
The methodology of coronary bifurcation angiography needs to be improved. Choosing the reference segment is a real issue that can induce errors in calculation. In the work of Schoenhagen et al on vascular remodelling of bifurcations, the reference segment was situated in the mother vessel for all calculations of daughter-vessel lesion remodelling20. Underestimation was therefore to be expected, and in point of fact the remodelling indices were consistently lower than 1.0:0.83 (considered as positive remodelling) for an unstable and 0.61 (considered as negative remodelling) for a stable clinical presentation. Each segment (mother vessel and daughter vessels) needs to be associated to its own reference segment. The references segments can then be calculated by the fractal law – which should be incorporated into angiographic quantification software.
Stent implantation and bifurcation
Costa et al recently reported IVUS findings in coronary bifurcations treated by the “crush” technique. Incomplete apposition of stent struts was seen in >60% of non-left main lesions17. Precise analysis of their IVUS data clearly reveals a stepwise difference between the proximal reference segment and the distal reference of the main (major daughter) vessel of 1.23 mm in the incomplete compared to only 0.34 mm in the complete stent apposition group. Thus, a simple calculation of the stepwise difference between the mother vessel and the major daughter vessel (generally referred to as the “main vessel” in intervention) enables such mechanically predictable incomplete apposition to be foreseen and corrected by proximal over-inflation by final kissing balloon dilation (see example in Figure 4).
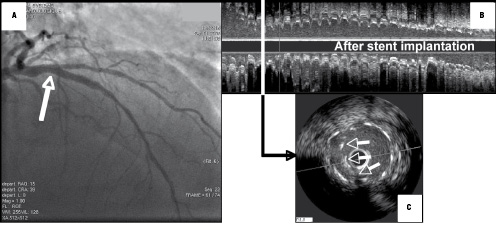
Figure 4. Detection of diffuse left main trunk atherosclerosis. On two angiographic views, the left main trunk showed no focal stenosis (A and B). Its measured diameter, however, was less than those of the daughter vessels: LAD and circumflex arteries. The real left main trunk diameter can easily be calculated as 4.22 mm [=0.678*(3.1+3.2)]: i.e., a relative obstruction of 50%. IVUS examination confirmed major diffuse atherosclerotic infiltration of the left main trunk (C). (The white star on the 4th IVUS cross section flags a plaque rupture undetected on angiography).
This linear law and the resultant fractal ratio provide an argument for generalising the practice of final kissing balloon inflation, originally developed to open side-branch struts and correct possible stent de-structuring in the part facing the side-branch. The mechanical rationale for final kissing balloon dilation found here probably accounts at least in part for the good results obtained21.
Bifurcation stent design
The requirements of coronary bifurcation management have gradually led companies to develop dedicated stents22. Their design should therefore take this fractal geometry on board, so as to avoid any foreseeable apposition defect due to discrepancies between real arterial diameters and the inflation criteria imposed by the diameter of the major daughter vessel.
Study limitations
Arterial bifurcations do not always divide into two but sometimes into three branches – known, then, as a “trifurcation”. This is rarely found in the coronary tree, and is most often not a true trifurcation so much as two successive contiguous bifurcations.
The most explicit models associate diameter and length and diameter and volume, so as best to describe the physiological behaviour of the coronary circulation. Our objective here was simpler, but above all much more pragmatic. We sought to derive an exact and reproducible parameter that would be easy to use in everyday interventional cardiology. The parameter in question is specifically valid for epicardial coronary arteries.
The angiograms were taken as normal, and IVUS exploration fully confirmed this assumption. Fractal ratio calculation of vessel diameter proved exact with respect to angiography to within 5%. In case of atherosclerosis, choosing a “normal” reference segment is inevitably subjective and imprecise23. In our own routine practice, however, the method proves efficient, despite its intrinsic limitations.
