Abstract
Aims: Defining vessel diameters and angles that comprise coronary side-branch intersections could assist in tailoring treatments to match anatomy, improve haemodynamic flow, and minimise mechanical trauma. We sought to characterise intersections of main vessels and side-branches by measuring actual diameters, angles, and shapes at the ostia in human coronary arteries.
Methods and results: Polymer casts were created using coronary trees from 23 adult cadaver hearts. Seventy-five arterial intersections between main vessels and side-branches were captured using the combination of a microscope (Smartscope MVP100) and computer program (Gage-X metrology software) specifically calibrated for video-based inspection and measurement (34-fold magnification). The intersection between main vessels and side-branches was a multifaceted, curvilinear transition rather than a bisecting angle. The shape of the ostia was typically elliptical rather than circular. Mean diameters were 2.88 mm in proximal main vessels, 2.34 mm in ostia, and 2.00 mm in side-branches (first-level branches). Obtuse proximal (150 degrees) and distal (111 degrees) angles with accentuated side-branch taper create a “barn door” effect with wider curvature at the bottom.
Conclusions: Matching treatments to these various forms of asymmetry at the main vessel-to-side-branch intersection may minimise injury and optimise scaffolding, and haemodynamic flow.
Introduction
Percutaneous coronary interventions were originally developed for the treatment of lesions in straight arterial segments. Since then, these devices and procedures initially intended for use in main vessel stenting have been applied to treating a variety of lesions including those at or near bifurcation junctions.1-4 Compared to a segment within a single vessel, the juncture between two vessels poses complexity for mechanical manipulations.5 Among the complicating factors are angulation, difference in vessel sizes, tortuosity, and underlying disease. Manipulations involving the side-branch (SB) and its junction with the main vessel (MV) are associated with a distinct set of ostial and SB complications. Specifically, SB procedural dissection, perforation, or acute occlusion may arise due to attempted wire, balloon, or stent passage and/or manipulations. Late restenosis may develop especially at the ostium or distal edge of the SB.
While consensus has been reached on how to classify the bifurcation lesions and the current treatments, less has been published about the underlying geometry of the vessels.6 Diameter and angle measurements have been made using a wide variety of imaging techniques and definitions including angiography, intravascular ultrasound, and computed tomography.7-10 A wide range of angles (30 to 137 degrees) have been reported at various branch-points along human coronary arteries depending on the study and methods.9-11 Angiographic measures can vary due to projections, bifurcation measurement algorithms, and definitions. Mismatches between stent features and the actual vessel diameters and angles could lead to vessel injury if over-sizing occurs or inadequate stent positioning if under-sizing occurs.
Resolution limits of the 2-dimensional angiographic imaging may obscure aspects of the 3-dimensional anatomy important for current percutaneous interventions. The purpose of this study is to characterise intersections of main vessels and side-branches by measuring actual diameters, angles, and shapes at the ostia in human coronary arteries.
Methods
We used retrograde aortic polymer injection to create casts of the human coronary tree in 23 adult cadaver hearts to characterise the anatomy of the SB vessels relative to the main branch vessels.
Coronary arteries
Cadaver hearts were acquired from Science Direct (Phoenix, AZ, USA) and the National Disease Research Interchange (Philadelphia, PA, USA). Protocols were reviewed and approved by the appropriate committees at each of the respective suppliers prior to shipment. Universal precautions were taken when handling the organs and remains were disposed of in an authorised manner.
Chemicals
A two-component, quick-cure acrylic polymer (#170-1000, Allied High Tech Products, Rancho Dominguez, CA, USA) was injected into the cadaver hearts to create the model. Sodium hydroxide (#221465) and potassium hydroxide (#221473) were obtained from Sigma Aldrich (St. Louis, MO, USA) and made into solutions up to 2M for tissue dissolution.
Model preparation
Hearts were received frozen and thawed prior to investigation. The aortas were cannulated and perfused retrograde with saline solution for at least 60 minutes. The polymer was mixed and injected retrograde into the aorta, filling both the aortic sinus and the coronary arteries. Hearts were then suspended for at least 60 minutes, allowing the polymer to cure completely. Models were subsequently immersed into sodium and potassium hydroxide solutions at 30° C for 24 hours to digest the tissue and rinsed in 20% bleach.
Coronary artery classification and characterisation
Detailed classification and measurement was completed on cast arteries estimated to be greater than 1.6 mm unless they had a substantial filling defect or had been broken during processing. The “first branch” was defined as the largest major bifurcation off each of the coronary arteries (LAD-DX1; LCX-OM1; and RCA-PDA); more distal branches were classified as “distal”.
Atherosclerotic disease was manifest as concave deformations formed by occlusive atheromas into the lumen as opposed to narrowing seen on the angiograms. Bifurcations were assessed using modification of existing angiographic classification systems for the casts: Medina classification for observable coronary disease6 and the Lefèvre system for plaque distribution and angulation.4
Geometric measurements
Coronary intersections between MVs and branches from the casts were captured using a Smartscope MVP100 inspection system and the Gage-X metrology software, a system specifically calibrated for video-based inspection and measurement (Optical Gauging Products Inc, Rochester, NY, USA). The lens of the microscope allows for 6.5:1 zoom with magnification to 135 times. Magnifications of 34 times or higher were selected to provide a detailed perspective between actual and histologic views. A custom fixture was used to hold and manipulate the models. Measurements were made with the bifurcation perpendicular to the field of view.
Figure 1A illustrates the locations of geometric measurements on a model vessel.

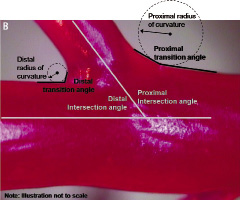
Figure 1. Location of vessel measurements. (A) Vessel diameters. (B) “Intersection” angles, “transition zone” angles, and radii of curvature. (See Table 3 footnote for definitions)
The centre of the bifurcation was defined as the point where all vessel centrelines met, given that centrelines represent the middle of the artery as defined by Ramcharitar and colleagues.12 Vessel diameters were measured as the width of the vessel perpendicular to the vessel centreline. In the MV, proximal diameter was measured 3 mm proximal from the centre of the bifurcation; similarly, distal diameter was measured 3 mm distal from the centre of the bifurcation. In the SB, SB diameter was measured 3 mm distal from the centre of the bifurcation. The ostial diameter was the distance between the inflection points of the MV and SB on the proximal and distal sides. The inflection point was defined as a change in slope when starting on the MV. Tapering in MVs was calculated by subtracting distal diameter from proximal diameter and dividing by the length between the two diameter measurements (i.e. taper length). For tapering in the SB, SB diameter was subtracted from the ostial diameter and divided by the taper length. Diameter measurements were used to derive fractal relationships, including linear law ratios, Murray law ratios and self similarity.7,13
Quantitative assessment of ostial shape required removal of the SB from the MV, thus destroying the cast, and was completed in a subset of six bifurcations. The SB was excised parallel to the MV at the take-off to avoid elliptical shapes due to the cutting angle. Qualitative grading of ostial shape as spherical or elliptical was made from cross-sections at 34-fold magnification. Orthogonal measurements of diameter were made to verify assessment of shape as spherical or elliptical based on differences of diameter >25%.
The “intersection” angle (analogous to that measured by angiography) was measured at the intersection of the centrelines of the MV and SB. The “transition zone” angle (as measured by computer-assisted imaging) was the initial angle in the MV-to-SB transition as measured from the MV (see Figure 1B). The radius of curvature was a best fit of the transition between the MV and SB on the proximal and distal sides.12
Two researchers were trained together in the defined data collection methods and example vessels were used to obtain consistent results. Each researcher then independently measured all bifurcations containing SB diameters estimated at greater than 1.6 mm. Data sets were then compared, and differences greater than 15% were jointly remeasured to ensure consensus.
Comparison to angiography in porcine hearts
Coronary cast model measurements were compared with quantitative coronary angiography (QCA) in a study of 67 porcine coronary segments coming from five different hearts. After completion of the angiogram, the porcine hearts were harvested and coronary cast models were made as described above. Measurements of coronary cast vessels (n=67) using the computer-assisted, video-based inspection system compared with measurements obtained using QCA had an average error of 6.65% ±5.76% with r=0.918. Hence, cast measurements were representative of those derived from matching angiograms.
Statistical analysis
Descriptive statistics were performed using Microsoft Excel to summarise vessel diameters, vessel taper, and angulation in the MV, ostium, and SB of donor heart models. Data are presented as mean±standard deviation (SD).
Results
Demographics and baseline lesion characteristics
Table 1 shows the demographic characteristics and primary causes of death for all cadaver donors.
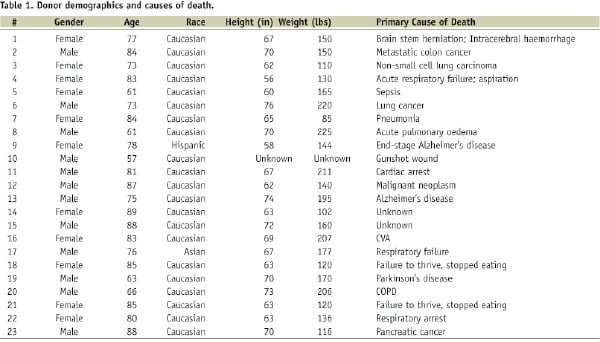
Only one donor died of cardiac causes. The absence of highly infectious diseases was confirmed by serology.
Among the 75 arterial intersections, 10 involved the left main coronary artery, 40 involved the first branch (largest, major bifurcation off the main vessel), and the remaining 25 involved more distal levels of branches. With respect to the presence of lesions, 43.5% of vessel intersections had no significant stenosis. By Medina classification, stenoses were located in the proximal MV in 20.3%, distal MV in 27.5%, and SB in 47.8%. By Lefèvre classification, stenoses were located predominantly in the SBs. Nearly all vessels were classified as Y-shaped (95.6%) and the most common Lefèvre stenosis type was Type 4 (30.4%).
Vessel diameter
Mean vessel diameters are shown in Table 2 categorised according to left main, first-level branches, and more distal branches.
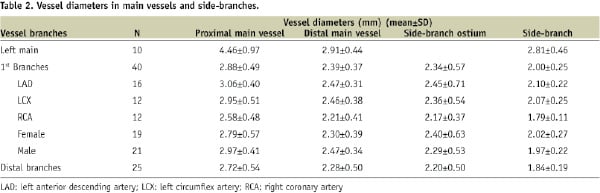
Left main diameters were the largest with a mean of 4.46 mm in proximal MVs and 2.81 mm in associated SBs.
In first-level branches, proximal MV diameters had a mean of 2.88 mm and a range of 1.75 to 3.82 mm. Distal MV diameters and ostial diameters were smaller, with means of 2.39 mm (range 1.78 to 3.16 mm) and 2.34 mm (range 1.34 to 3.90), respectively. The smallest diameters were within the SBs, where a mean of 2.00 mm was flanked by a narrower range (1.68 to 2.59 mm). The mean diameters in the distal MV and the ostium were similar, varying by only 0.05 mm. Yet, the difference between proximal MV diameter and the SB diameter was 0.88 mm.
In more distal branches, the mean proximal MV diameter of 2.72 mm (range 1.78 to 3.93 mm) was smaller than in first-level branches by 0.16 mm. Distal MV diameters and ostial diameters were also smaller with means of 2.28 mm (range 1.67 to 3.50 mm) and 2.20 mm (range 1.33-3.12), respectively. Finally, the mean diameter in these SBs was only 1.84 mm (range 1.59 to 2.27).
Vessel taper and branching
Calculations of vessel taper and associated branching calculations are listed in Table 3.
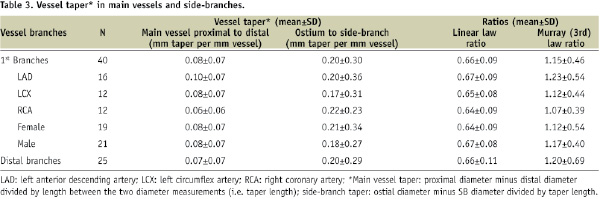
In first-level branches, tapering within the MV was markedly more gradual with a mean 0.08-mm decrease per mm of vessel calculated over a distance of 6 mm. In contrast, the tapering from the ostium to the SB had a larger mean of 0.20 mm decrease per mm of vessel calculated over a distance of 1.75 mm. As shown in Table 3, the patterns of vessel tapering in the more distal branches were similar to those observed for first-level branches.
Using diameter measurements from the human casts, ratios were obtained using two of the most common theoretical formulations of fractal relationship, the linear law7 and Murray’s law (cost function relation).14 The calculated linear law average ratio was 0.66±0.09 for first-level branches, with a range of 0.64 to 0.68 across vessels grouped by vessel or gender (Table 3). Extending the analysis to more distal bifurcations anywhere in the heart, ratios ranged from 0.62 to 0.71 when grouped by vessel or gender with an average of 0.66±0.11. Similarly the average Murray’s law ratio for first-level branches was 1.15±0.46 (range 1.07 to 1.24 across subgroups) and when extended to more distal bifurcations was 1.20±0.69 (range 0.94 to 1.53 across subgroups). Values for both ratios across all bifurcation levels and subgroups were relatively constant.
The relative reductions between MV diameter and daughter vessel diameters were calculated. For the distal MV (major daughter) branch, there was a 17% diameter reduction in the first-level branches and 16% reduction in more distal branches. The SB had a 30% diameter reduction in the first level and a 32% reduction in other vessels. As with the taper measurements, SB daughter vessels demonstrated a larger relative decrease in diameter as compared to distal MVs with percentage decreases preserved across branching levels.
Bifurcation angles
When examined at the 34-fold magnification of computer-assisted video inspection, the SB take-off from the MV was actually a transition zone composed of a series of angles that formed the curve reflection at the base of the ostium. In other words, as illustrated in Figure 2, the actual geometry of the take-off was curvilinear rather than a bisecting angle.
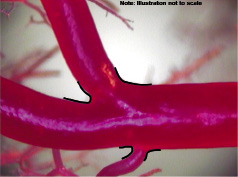
Figure 2. Curvilinear transitions (denoted by black curved lines) rather than bisecting angles characterising the main vessel-to-side-branch connection.
Intersection angles and transition zone angles are shown in Table 4.
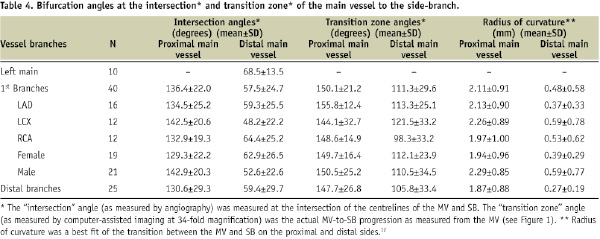
For the left main, only the angle between the LAD and LCX could be measured yielding a mean of 68.5°±13.5° (n=10). The distributions of individual angle measurements based on centreline measurements (intersection angle) and local measurements (transition zone angle) are depicted in Figure 3.
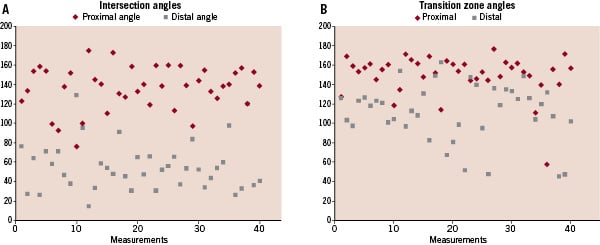
Figure 3. Distribution of values for (A) intersection angles (similar to angiographic) and (B) transition zone angles measured by computer-assisted imaging at 34-fold magnification.
For intersection angles, proximal angles were predominantly obtuse at the first level (mean: 136 degrees; range: 77 to 174 degrees) with a 2.5-fold larger angle than distal angles (mean: 58 degrees; range: 17 to 129 degrees), which were predominantly acute. These findings were consistent with the radius of curvature, another measure of angulation, where the proximal mean was 2.11 mm and the distal mean was 0.48 mm.
When looking at transition zone angles, the difference between proximal and distal angulation was less dramatic. The proximal angle mean of 150 degrees (range: 58 to 177 degrees) was obtuse at the first level as was the distal angle mean of 111 degrees (range: 46 to 163 degrees). These localised measurements within the transition zone revealed angulations substantially different from the more global intersection angles measured by QCA. Transition zone angles remain fairly constant across a range of intersection angles. For example, intersection angles of 30°±15° had proximal transition zone angles of 154.8°±30.4°, similar to intersection angles of 60°±15° with transition zone angles of 150.8°±14.6° and intersection angles of 90°±15° with transition zone angles of 143.6°± 14.0°.
Ostial geometry
The shape of the ostial lumen area after cutting off SBs was classified as elliptical (Figure 4A) in five and spherical in one of the six vessels examined. These classifications were confirmed by the perpendicular diameter measurements where five out of the six had corresponding differences between the two diameters averaging 25%. This ostial asymmetry contrasts with the symmetric roundness typically observed in cross sections of MVs and SBs. The cartoon in Figure 4B illustrates how the various aspects of asymmetry come together to create a “barn door” effect with the oval shape, wider bottom angles, and more dramatic SB taper.

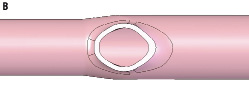

Figure 4. Ostial geometry. (A) Cross-section of human coronary artery cast showing oval shape. Note: distal narrowing in the vessel is characteristic of vessel stenosis in cast models. (B) Illustrations of an oval ostium in cross section and the subsequent “barn door” effect observed from a lateral view.
Discussion
The novelty of this study derives from using computer-assisted imaging methods to analyse casts of human coronary artery bifurcations with an intermediate degree of magnification (34-fold) that is greater than QCA but less than histology. With histology, 15 to 20 micron samplings of cross sections are viewed, whereas, the cast analysis provides an integrated 3-dimensional perspective of the artery. Analysis of 75 cast intersections demonstrates a complex, 3-dimensional transition zone between MV and SB. First, the intersection between the MV and SB involves a multifaceted transition that is curvilinear rather than the commonly employed analogy of two straight tubes intersecting. Second, the shape of the ostium is typically elliptical and not circular as is often portrayed. Third, narrowing or taper along the length of the SB is 2.5-fold greater than that seen in the MV. Fourth, at the magnification studied, the proximal and distal SB take-off angles are both obtuse, as opposed to complimentary obtuse and acute angles, resulting in the observed “barn door” effect.
Implications of asymmetrical ostial geometry
Coronary stents were originally developed for use in discrete, focal lesions in straight vessel segments where the anatomy was fairly symmetric. Most references to asymmetry in the coronary tree arose in the context of haemodynamic flow and branching; less is published on anatomic asymmetry.8,9 One of the most interesting findings in this cast analysis, is that the shape of the SB take-off from the MV is not circular but oval or elliptical. Our finding in epicardial coronary arteries extends the report by Zeina et al in left main coronary arteries, in which computer tomographic analysis demonstrated that 66 of 70 sections at the level of the ostium had an elliptical shape.15 Interestingly, the obtuse proximal and distal angles together with the accentuated SB taper in the intersection between the MV and SB create a “barn or storm door” effect (B). Specifically, the entryway (ostium) is taller at the top than it is wide and the curvature is wider at the bottom than at the top.
The accelerated taper from the ostium to the SB presents challenges in balloon and stent sizing given the diameter differences in the proximal and distal segments of the SB. Expansion of a stent-balloon system to adequately appose the struts in the proximal section of the SB could over-expand the distal section leading to vessel injury, dissection, or edge stenosis. Conversely, a stent small enough to safely dilate the distal aspect of the SB would likely be inadequately apposed in the wider ostium even if final “kissing balloons” dilatation is performed.
If traditional symmetric, tubular stents were used in a zone with these forms of asymmetry, one could anticipate a mismatch between stent and vessel shapes resulting in incomplete apposition in some areas and strut protrusion in others. These mismatches might lead to uneven or unpredictable scaffolding, multiple metal layers in cases when two stents are used, strut wall injury, or mural thrombosis between the struts and vessel wall. These factors compounded by altered haemodynamic flow may explain why the ostium is often the site of restenosis after bifurcation stenting.
Diameter measurements in perspective
Most recent studies of coronary dimensions, branching, and angles have used imaging modalities, such as coronary angiography, intravascular ultrasound and computerised tomography.7 In this study of measurements taken directly from human coronary casts, mean MV diameter was 2.88 mm with mean ostial diameter in first-level SBs of 2.00 mm. In contrast, using quantitative coronary angiography, Finet and colleagues reported larger mean diameters for the main (mother) vessel of 3.33 mm with first SB diameters of 2.70 mm.7 However, in the Finet study, 45 bifurcations were in vessels with diameters larger than 4.0 mm, likely reflecting left main bifurcations. In our study, mean LM diameters were larger at 4.46 mm with SB diameters of 2.81 mm. With left main measurements excluded from the Finet study, the average diameter for all vessels would likely approximate the results of this study where left main measurements were considered separately from other first-level branches. Differences between the two studies may potentially be explained by the range of vessels included, inclusion of left main arteries, measurement site(s) along the artery, distortions with angiographic views or by coronary cast generation, and patient population. Perhaps the most likely contributor to measurement differences is the longitudinal position at which arterial measurements were taken, particularly given the presence of vessel taper.
Branching
Comparisons of branching parameters showed self-similarity across branching levels in this study and linear law ratio levels that were comparable to previously published reports.7 For this cast analysis, the average calculated linear law ratio was 0.66 for the first-level branches, which is similar to the 0.678 (all vessels) or 0.654 (2.5 to 3.0 mm vessels) reported by Finet et al.7 The average Murray law ratio14 was 1.15 in the cast analysis, confirming the pattern of fractal geometry or self-similarity at bifurcations. Unique geometric aspects of the branching are emphasised here. A simple linear law continues to suffice in describing the relative relationship between vessels. This argues that preserving the division of flow at a bifurcation can be an important component of treatment. A degree of asymmetry can be attributed to the fractal branching, both in the flow distribution pattern and in the ratio of daughter branch diameters.8,16
Insights regarding angle measurements
In published literature describing bifurcation angles, methodology is insufficiently described to discern the precise point where measurements were taken.8,15 In this manuscript, we show that measures can vary by 50 degrees or more dependent on the scale of observation (i.e. 34-fold magnification vs QCA) and methods used. For example, the distal intersection angle, which is similar to that used for angiographic assessment was 54 degrees compared to the distal transition angle of 111.3 degrees. More uniform definitions and precise methods for measuring angles would facilitate comparisons across studies and technologies. Interestingly, we found that the higher-resolution transition zone angles were relatively constant across a range of angiographic angles, supporting the concept of a “barn door” type transition zone that is independent of angiographic angle.
Study limitations
A study using human casts as the basis for analysis relies on measurements that represent a moment of full perfusion in the arteries without compressive effects of the cardiac cycle. Of note, angiographic measurements are typically taken from specific frames, which also represent a fixed moment in time. The measured ostial taper zone was short (1.75 mm) as it was confined to the transition between the MV and SB ostium. Hence, quantitation in this area will be sensitive to error due to its dependence on ostial length. Additionally, because the heart is cast post-mortem, the accumulation of active substances or degradation of cellular components could lead to changes not present in vivo. Moreover, manipulation of the heart during curing could introduce local artifacts (incomplete polymer filling or cast breaks) reducing the sample size. The sample size of 23 hearts might be considered small for an imaging study, though it is sizable for a cadaveric study. The actual number of bifurcations analysed, however, was 75, indicating that smaller side SBs were studied than would be seen in studies focused on the larger-diameter first and second daughter branches that are often clinical targets.
Clinical implications
The simple approach of examining actual human coronaries to better define the geometry at the MV-SB intersection shows a complex transition zone with a curvilinear intersection, elliptical SB take-off shape, contrasting proximal and distal angles between MV and SB, and differential taper in the SB compared with the MV. Furthermore, the ostium of a bifurcation SB has its own unique asymmetric, “barn door” geometry and taper that is not always apparent using traditional imaging modalities. Given these forms of asymmetry, one could surmise that use of symmetric, tubular structures as scaffolding at the intersection would be associated with either distortion of the stent or the anatomy. Efforts to better match the scaffolding system to the asymmetric ostial anatomy may minimise implant injury, enhance scaffolding, and improve haemodynamic flow and long-term restenotic outcomes.
Acknowledgements
The authors thank Jesse Rios for contributing to model development, Steven Cai for performing bifurcation measurements, Science Direct and National Disease Research Interchange for the procurement of tissues, and Laurie LaRusso, MS, ELS, for her contribution to the writing of this manuscript.

