Abstract
Aims: The size of stent cells is an important design parameter influencing the resulting wall coverage and strut positioning of several bifurcation stenting techniques. Therefore, we report accurate geometrical information on stent cell size of five different stents with the key purpose to assist with stent selection for bifurcation lesions.
Methods and results: We developed an innovative technique to assess cell size with high accuracy based on micro-CT images. In addition, the size of the ostium was calculated for several idealised bifurcations with a cylindrical main and side branch. The cell circumferences of the investigated stents vary substantially, with values between 9.5 and 19.8 mm (or an equivalent maximal cell diameter between 3.0 and 6.3 mm). Comparison of these cell circumferences with the calculated ostium circumferences shows which stents should preferably be used for which bifurcations, as these stents have cells that can be sufficiently enlarged by dilating through the side.
Conclusions: The cell sizes of the investigated stents differ considerably. This should be taken into account when applying a particular bifurcation stenting technique. The risk on limited main or side branch patency due to obstructing stent struts can be minimised by using the reported data for stent selection.
Introduction
Stenting coronary bifurcation lesions is still associated with higher restenosis rates compared to conventional stent implantation, even in the drug-eluting stent era1. Adequate wall coverage and good positioning of the stent struts against the vessel wall are considered as two crucial factors for successful bifurcation stenting1,2. This can be accomplished by applying a suitable stenting technique and using an appropriate stent design. Selecting a stent design with a sufficiently large cell size reduces the possibility of compromising the main or side branch lumen. For example, stent placement in the main branch is often followed by inflating a balloon through the side of the stent in order to improve the side branch lumen (and sometimes to create access for subsequent stent placement in the side branch). In this case, the size of the cell through which the balloon is inflated should preferably be as large as the side branch ostium (Figure 1, panel A). The same condition applies to stents used during the so-called “crush” procedure. This is a technique which should be ended by kissing balloon postdilatation3 to obtain optimal deployment (Figure 1, panel B). The cell opening also plays a major role for culotte stenting, during which a stent is implanted in the proximal part of the main branch and in the side branch. Kissing balloon postdilatation is often performed to optimise the downstream lumen. To achieve optimal results, the cell size of this stent should preferably be as large as the cross-section of the main branch (Figure 1, panel C).
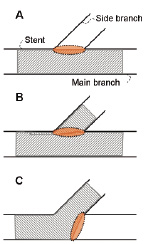
Figure 1. Stent cell requirements for different stenting strategies (the zone of interest is indicated with a dotted line). When performing provisional bifurcation stenting, the stent cells should be at least as large as the side branch ostium (panel A). The same condition is valid for both the side and main branch stent during crush stenting (panel B). The situation as shown in panel C is encountered during culotte stenting and in this case, the cells should be at least as large as the cross-section of the main branch.
The size of stent cells has already been reported in previous studies, based on data provided by the manufacturers4, or by measuring the width and height of expanded stent cells5,6. To our knowledge, an independent method to measure stent cells with high precision has not been proposed yet. Therefore, we describe a methodology to accurately quantify the cell circumference of stents based on micro-CT scans. Furthermore, the size of the ostium is calculated based on diameter and angle information for several bifurcation geometries. Combining cell size with anatomical information may assist to select the appropriate stent design for the applied treatment technique and for the particular patient.
Materials and methods
Investigated stents
The cell circumference was determined for the following five “3 mm” stents: the sirolimus eluting Cypher (8 mm length, Cordis, Johnson & Johnson, Warren, NJ, USA), PRO-Kinetic (18 mm length, Biotronik, Berlin, Germany), the paclitaxel eluting Taxus Liberté (32 mm length, Boston Scientific, Natick, MA, USA), the everolimus eluting Promus (12 mm length, Boston Scientific, Natick, MA, USA) and the ABT-578 eluting Endeavor (12 mm length, Medtronic, Minneapolis, MN, USA ) stent. The Cypher and Taxus Liberté stent are stainless steel stents, while the others are made of the stronger cobalt chromium alloy. The PRO-kinetic stent is coated with a silicon carbide layer. The Promus stent uses the Multi-Link Vision stent platform and is identical to the Xience V stent (Abbott Vascular, Redwood City, CA, USA).
Micro-CT
All stents were scanned as delivered by the manufacturer in their crimped, balloon-mounted state. In order to obtain accurate results on the stent cell dimensions, only 8 mm of the total stent length was scanned using a Varian Paxscan 2520V X-ray amorphous-Si flat panel detector with 1536x1920 pixels of 127 µm. With a magnification factor of 34, this results in a CT voxel size of 4.3 µm. The in-house built high resolution set-up at the UGCT facility7 used for this investigation consists of a Feinfocus open type X-ray tube (Xylon/Feinfocus, Comet Group, Flamatt, Switzerland) with transmission target and a sample manipulator with air bearing rotation stage. The X-ray tube was used at 100 kV and 2.7 W with the resolution of this total system under 2 µm. The scans consisted of 600 projection images (0.8 sec integration time) that were reconstructed using Octopus reconstruction software developed at UGCT8. The resulting dataset of cross-sectional images was imported into Mimics (Materialise, Leuven, Belgium) where a triangulated surface mesh of the stents was created and exported in the stl format.
Cell circumference determination
The triangulated surfaces representing the stents outer surfaces were imported in pyFormex, open-source software (http://pyformex.berlios.de/) currently under development at our institution. pyFormex is a tool for generating, manipulating and operating on large geometrical models of 3D structures by sequences of mathematical transformations. The stent geometries were unrolled by transforming the coordinates and were cut by a plane after selection of a smaller zone in order to obtain planar line segments. Subsequently, a cell was selected for each stent from the resulting collection of two-dimensional lines and used to determine the cell circumference. This cell circumference was then used to calculate the corresponding maximum achievable diameter (Dmax) of the cell opening that can be obtained upon inflation of a balloon through the side of the stent. This Dmax is equal to the cell circumference divided by pi.
Calculation of ostium circumference
The ostium circumference was determined for idealised bifurcations with a cylindrical main and side branch starting from a parametric description of the ostium, which is the three-dimensional line indicated in Figure 2.
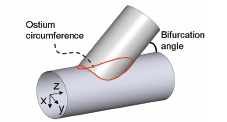
Figure 2. The size of the ostium depends on the bifurcation angle and the side and main branch diameters. The ostium is described by a three-dimensional curve from which the circumference can be calculated.
The ostium was written as a function of the main branch axial position: x=f(z) and y=f(z) with z the main branch axis. Subsequently, the ostium circumference was calculated as the sum of the length of infinitesimal small line segments. The resulting circumference depends on the main and side branch diameters and on the angle of intersection.
Results
Cell circumference
The different steps of the cell circumference measurement procedure are shown in Figure 3 for the Cypher stent.
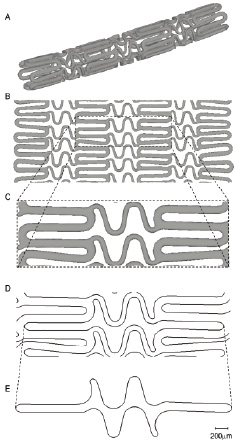
Figure 3. Demonstration of the complete procedure to obtain a single cell of the Cypher stent. The cell circumference can then easily be calculated as the sum of the length of all planar line segments of this cell.
Panel A shows the triangulated surface obtained after reconstruction and segmentation of the micro-CT images. A mathematical transformation of the coordinates of all triangles results in an unrolled stent geometry (panel B), which is still three-dimensional. Subsequently, a small zone containing one cell is selected (panel C). The planar line segments depicted in panel D are obtained after intersection of this three-dimensional geometry with a plane. This can then be used to select a single cell and to calculate its circumference, as shown in panel E.
Applying the same methodology to the other stents results in the planar cells shown in Figure 4.

Figure 4. Comparison of microscopic images with the resulting planar representations of the cells. The microscopic images do not have the same scale. From top to bottom: Endeavor, PRO-Kinetic, Promus and Taxus Liberté stent.
The cell circumferences and the corresponding maximum achievable diameters of the different stents are summarised in Table 1.
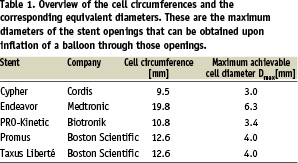
The cells of the Cypher stent have the smallest circumference (i.e. 9.5 mm or Dmax=3.0 mm), whereas the Endeavor stent has the largest openings (circumference=19.8 mm or Dmax=6.3 mm).
Ostium circumference
The ostium circumference is displayed as a function of the angle of intersection for a 3 mm main branch (Figure 5).

Figure 5. The ostium circumference of a 3 mm parent vessel is shown as a function of side branch diameter and the bifurcation angle.
The results are shown for three possible side branch diameters (i.e. 2.25, 2.50 and 2.75 mm).
Discussion
Cell circumferences of the studied DES designs differ considerably, with values ranging from 9.5 to 19.8 mm or with a maximal achievable cell diameter (Dmax) varying between 3.0 and 6.3 mm. These stent openings play an important role, especially during bifurcation stenting4,5. For example, dilating a balloon through the side of a main branch stent with openings that are too small will fail to completely restore the side branch lumen due to obstructing stent struts. Struts not in contact with the vessel wall should be avoided as this may cause thrombus formation2. The large variation of the cell sizes of the investigated stents are explained by the different design concepts. The Cypher stent is a typical example of a closed cell design, whereas all other stents can be classified as open cell designs.
Combining cell size with anatomical data may assist to select a stent for a given bifurcation stenting problem. This requires knowledge of the ostium circumference, which, as we have shown, can be mathematically calculated when idealising the bifurcation geometries with a cylindrical main and side branch. Real-life bifurcations will certainly have a more complex anatomy9 (e.g. ostial calcification and/or tortuosity), but these calculated values are still valuable as they are at least indicative and provide an idea of the order of magnitude. In the idealised case, the ostium circumference depends on the main and side branch diameter and on the angle of intersection. The relation between the angle and the ostium circumference is clearly nonlinear (Figure 5) as the circumference varies more rapidly at small angles. This indicates that special attention should be paid to the selection of a stent which will be implanted in the main branch of a small angled bifurcation. In Figure 6, the stent cell circumferences are plotted on these graphs.
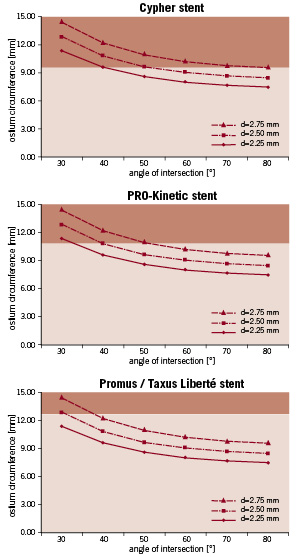
Figure 6. The dark zones indicate the cases in which the ostium circumference is larger than the cell circumference when the stents are deployed in a 3 mm main branch (for three different side branch sizes). For example, when a Cypher stent is implanted in a bifurcation with a 3 mm main branch, 2.5 mm side branch and a 40 degree angle, the ostium circumference (10.8 mm) is larger then the cell circumference (9.5 mm). Therefore, it is highly likely that in these cases (i.e. cases within dark zone) the cells will not be sufficiently enlarged by balloon dilatation through the side. The Endeavor stent is not shown because the cells can be sufficiently enlarged in all cases.
The dark zones show the cases in which the ostium circumference is larger than the cell circumference when the stents are deployed in a 3 mm main branch (for three different side branch sizes). For example, when a Cypher stent is implanted in a bifurcation with a 3 mm main branch, 2.5 mm side branch and a 40 degree angle, the ostium circumference (10.8 mm) is larger then the cell circumference (9.5 mm). Therefore, it is highly likely that in these cases the cells will not be sufficiently enlarged by balloon dilatation through the side (and final kissing balloon postdilatation) and that not all stent struts will be in contact with the vessel wall.
The presented cell data are also useful for stents partially deployed in the main and side branch as encountered during culotte stenting. These stents should preferably have cells with a Dmax greater than the distal main branch diameter. If this condition is not respected, it is highly likely that gaps will occur between some struts and the vessel wall.
Accurate geometrical information of the bifurcation (main and side branch diameters and angle) is very important in order to apply the presented stent selection method in clinical practice. The most critical parameter is the angle of intersection. Dedicated software may help to accurately determine this bifurcation angle10.
Selecting stents with large openings will reduce the risk of limited side (or main) branch patency after dilating through the side, but using such stents may result in inferior wall scaffolding/coverage and larger tissue prolapse11. Besides the stent cell size, a large number of other stent properties influence the choice for a particular stent, such as flexibility, conformability, trackability and radial strength. Furthermore, such careful selection based on cell size does not guarantee optimal stent deformation as these stents are not developed to treat bifurcation lesions. There is clearly a need for dedicated devices allowing easy and safe treatment while providing optimal scaffolding and minimising luminal obstruction.
Limitations
Although the proposed method gives additional information to interventional cardiologists, it should be stressed that selecting an appropriate stent is more complex than depicted by mathematical modelling. For example, bifurcation angles may change following stent implantation. In addition, stent selection in clinical practice is based on a large number of design aspects and cell size is just one of them (e.g. flexibility, radial strength, etc.).
It has been shown that strut rupture may occur after side-branch dilatation2 at high pressures using a large balloon (e.g., 4 mm nominal diameter). Such behaviour is not taken into account by the proposed methodology, which uses the original (non-ruptured) cells as input. However, strut rupture should be avoided since it has been suggested for peripheral vessels that stent fracture is related to higher restenosis rates12.
The proposed criterion to select stents with a cell circumference which is larger than the ostium circumference is too strict in case of partial stent deployment within the side branch as demonstrated in Figure 7.
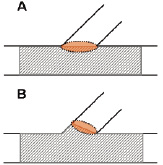
Figure 7. Panel A shows the worst-case situation which was used in this work (no partial stent deployment in the side branch). This situation requires larger cells (at least as large as ostium) than in case of partial stent deployment in the side branch (panel B).
This means that the criterion is worst-case and guarantees the selection of stents with sufficiently large openings independent of the deployment behaviour of the stent (partial deployment within side branch or not).
Conclusions
We applied an innovative measurement technique based on micro-CT images to assess cell sizes of five 3 mm stents, and observed a considerable variation. This should be taken into account when applying a particular bifurcation stenting technique for a specific lesion as the selection of a stent with cells that are too small will inherently lead to suboptimal deployment and obstructing struts.
Acknowledgements
Peter Mortier’s research is supported by a BOF-grant (01D22606) from Ghent University, Belgium.

